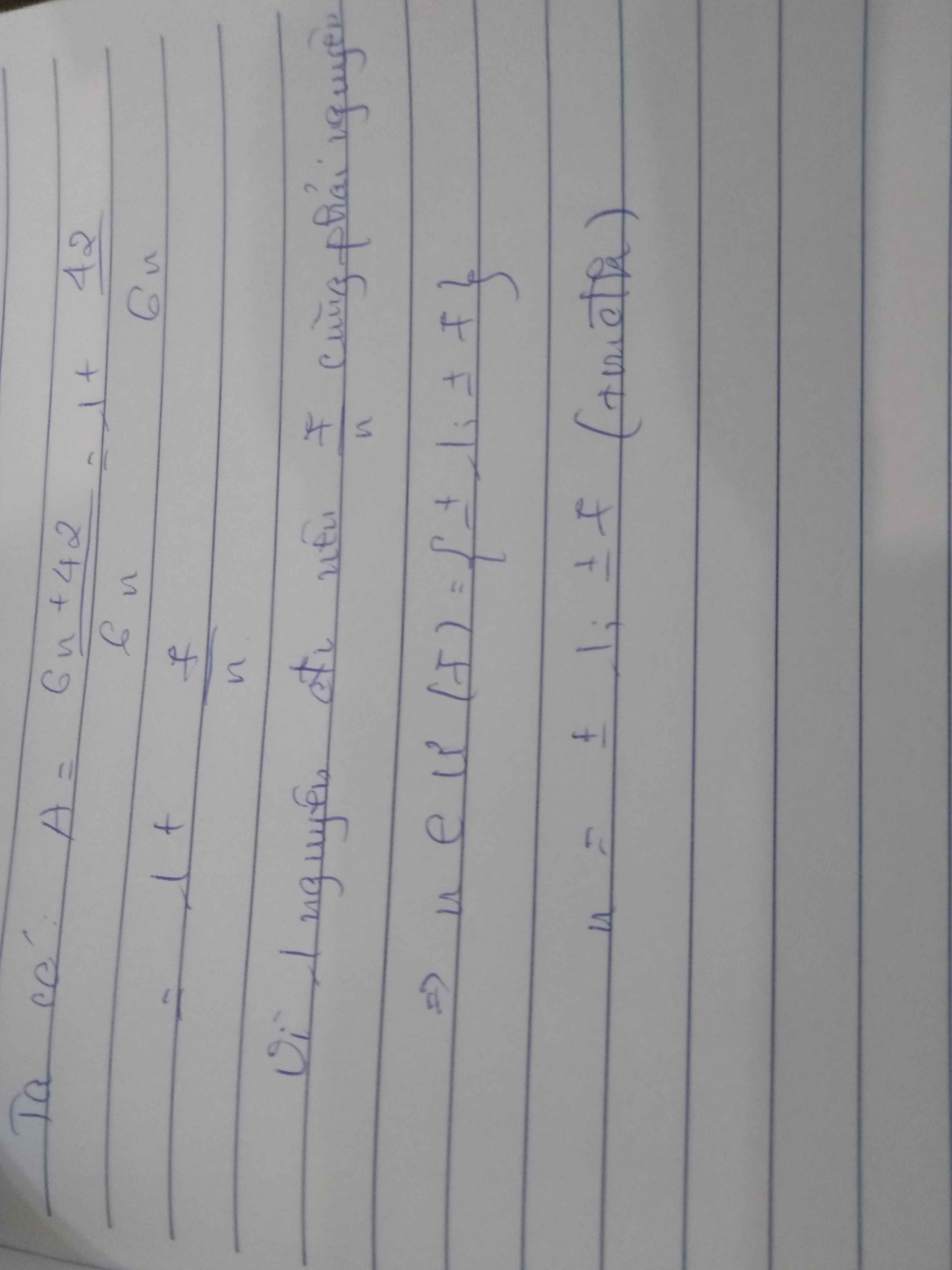Trong số nguyên tố : a = 3 ; 9

vì 232 chỉ có 2 ước

  239 chỉ có 2 ước

còn các số khác : trong các chữ số đều là hợp số .

vậy a = 3;9

Theo bảng số nguyên tố bé hưn 1000, ta thấy:

Có 2 số nguyên tố theo dạng \(\overline{23a}\)là: 233 và 239

Vậy a = 3; 9

ta có:23 là số nguyên tố

nếu : 23.a là số nguyên tố thì a  thuộc {1}

thây a là 1

thì : 23.a=23.1=23 

23 là số nguyên tố

Ta có 23 là số nguyên tố. Để 23*a là số nguyên tố thì a phải là 1

23*1=23

23 là số nguyên tố

Vì a là chữ số hàng đơn vị nên:

a thuộc { 0;1;2;....;9}

Nếu a thuộc { 0;2;4;6;8} thì 23a chia hết cho 2 mà 23a>2

=> 23a là hợp số (trái giả thiết) ( loại)

- Nếu a=5 thì 235 chia hết cho 5 và 235>5 nên 235 là hợp số (trái giả thiết) (loại)

- Nếu a thuộc { 1;7} thì 23a chia hết cho 3 mà 23a>3 nên 23a là hợp số (trái giả thiết) (loại)

- Nếu a thuộc {3;9} ta có: 233;239 là các số nguyên tố

bạn vào câu hỏi tương tự

****

giở lại trang cuối của SGK toán tập 1

a) A=2;3;5;...

b) A= 4;6;8;...

c) A=1

Để A là số nguyên thi 6n+42⋮6n

6n⋮6n⇒42⋮6n

7⋮n

n∈Ư(7)={1;-1;7;-7}

Vậy n ∈ {1;-1;7;-7}

a = 3, a=9

a = 3 hoặc a = 9

( Bảng thừa số nguyên tố cuối sách giáo khoa Toán 6 trang 128 )

Nhớ k cho mk nhé! Thank you

a có  thể là 3 hay bằng 9

Lời giải:

$n^2+12n=n(n+12)$ nên để $n^2+12n$ là số nguyên tố thì 1 trong 2 thừa số $n, n+12$ bằng $1$, số còn lại là số nguyên tố.

Mà $n< n+12$ nên $n=1$

Khi đó: $n^2+12n=1^2+12.1=13$ là số nguyên tố (thỏa mãn)