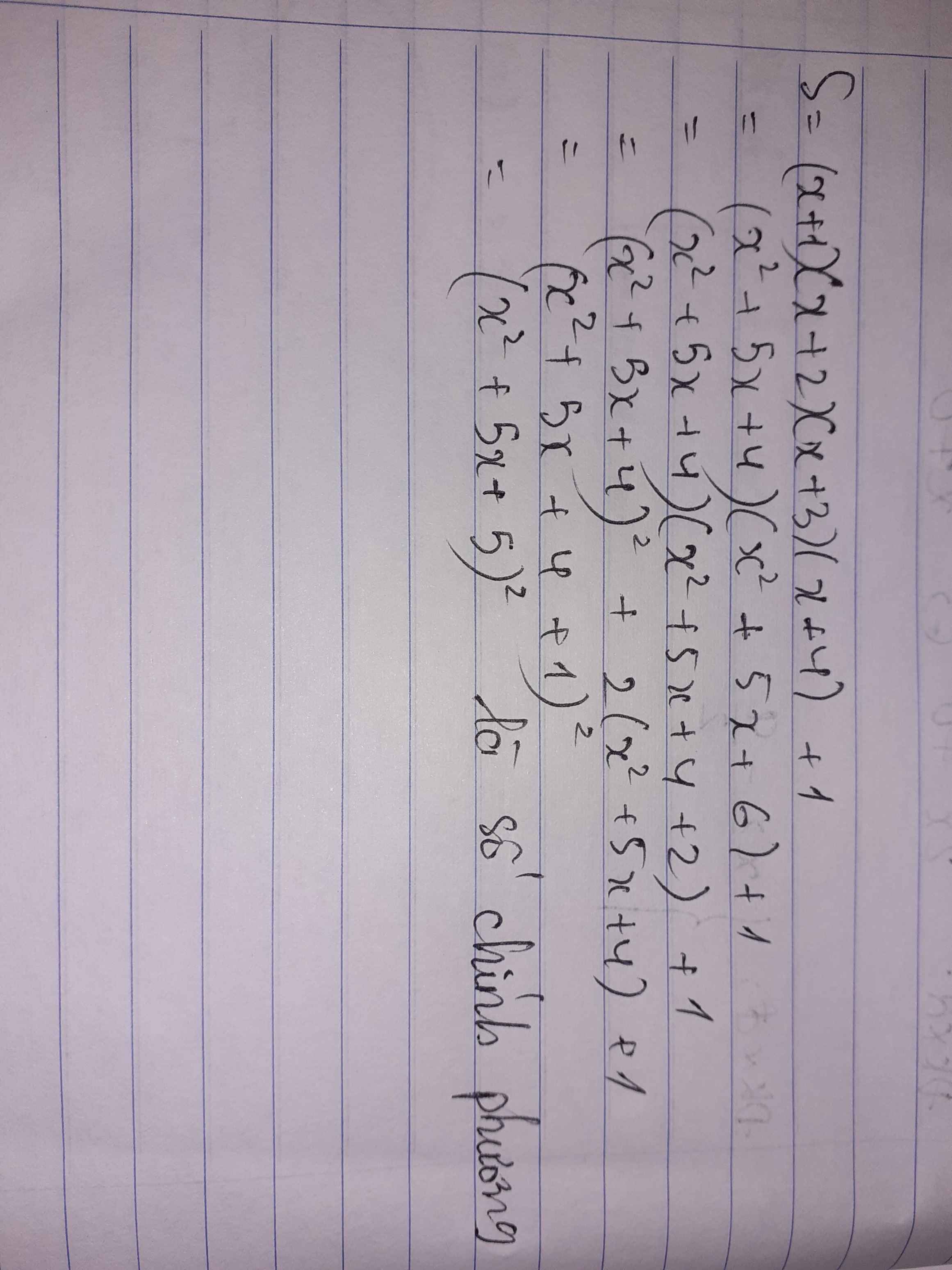Cmr:S=1/4^1+1/4^2+....+1/4^2017<1/3

Những câu hỏi liên quan
CMR: 1/151+1/152+1/153+…+1/300=1-1/2+1/3-1/4+…+1/299-1/300
CMR:S=1/2+1/3+1/4+…1/2013
Sn=[1/(1*2*3*4)]+[1/(2*3*4*5)]+...+{1/[n*(n+1)*(n+2)*(n+3)]}.CMR:Sn<1/18
\(S=\dfrac{1}{5^2}+\dfrac{1}{5^4}+...+\dfrac{1}{5^{2022}}.CMR:S< \dfrac{1}{24}\)
\(S=\dfrac{1}{5^2}+\dfrac{1}{5^4}+...+\dfrac{1}{5^{2022}}\)
=>\(25\cdot S=1+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2020}}\)
=>\(25S-S=1+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2020}}-\dfrac{1}{5^2}-\dfrac{1}{5^4}-...-\dfrac{1}{5^{2022}}\)
=>\(24S=1-\dfrac{1}{5^{2022}}\)
=>\(S=\dfrac{1}{24}-\dfrac{1}{24\cdot5^{2022}}< \dfrac{1}{24}\)
Đúng 1
Bình luận (0)
cho S=1/16+1/36+1/64+...+1/(2n)2 CMR:S<1/4
CMR:
S=(x+1)(x+2)(x+3)(x+4)+1 luôn luôn là 1 số chính phương ∀ x ∈ Z
\(S=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+4+2\right)+1\)
\(=\left(x^2+5x+4\right)^2+2\left(x^2+5x+4\right)+1\)
\(=\left(x^2+5x+4+1\right)^2\)
\(=\left(x^2+5x+5\right)^2\) là SCP (đpcm)
Đúng 3
Bình luận (0)
\(S=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt \(t=x^2+5x+5\Rightarrow\) pt trở thành \(\left(t-1\right)\left(t+1\right)+1=t^2-1+1=t^2\)
\(=\left(x^2+5x+5\right)^2\)
Vì \(x\in Z\Rightarrow x^2+5x+5\in Z\Rightarrow\left(x^2+5x+5\right)^2\) là số chính phương
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
CMR:S=\(\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< 1\frac{2}{3}\)
CMR:S=1+3+32+...+32011chia hết cho 4
Ta có S=1+3+3^2+...+3^2011 chia hết cho 4
=(1+3)+(3^2+3^3)+...+(3^2010+3^2011)
=1.(1+3)+3^2.(1+3)+...+3^2010.(1+3)
=1.4+3^2 .4+...+3^2010 .4
=4.(1+3^2+...+3^2010) chia hết cho 4
Vậy: S chia hết cho 4
Đúng 0
Bình luận (0)
CMR:S=1+3+32+.....+32011 chia het cho 4
S= 1 + 3 + 32 +..+399
a, CMR:S \(⋮\)4
b, CMR:S\(⋮\)40
CẢM ƠN MN GIÚP ĐỠ
S = 1 + 3 + 32 +..+399
=> S = (1 + 3) + ... + (3^98 + 3^99)
=> S = (1 + 3) + ... + 3^98.(1 + 3)
=> S = 4 + ... + 3^98.4
=> S = 4.(1 +... + 3^98) chia hết cho 4 (Đpcm)
Đúng 0
Bình luận (0)