cho tam giác ABC, đường trung tuyến AM. CMR: nếu cotB=3cotC thì AM=AC.
c
cho tam giác ABC, đường trung tuyến AM. CMR: nếu cotB=3cotC thì AM=AC.
giải thích do hộ mik cảm ơn nhiều =))
\
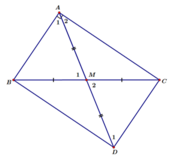
Kẻ đường cao AD.
Theo đề: \(cotB=3cotC\Rightarrow\dfrac{DB}{AD}=3.\dfrac{CD}{AD}\Rightarrow DB=3CD\)
\(\Rightarrow BC=4CD\) mà \(BC=2CM\Rightarrow CM=2CD\left(1\right)\)
Vì \(BD=3CD\Rightarrow BD>CD\Rightarrow AB>AC\)
\(\Rightarrow D\) nằm giữa M và C (2)
Từ (1) và (2) \(\Rightarrow D\) là trung điểm MC
mà \(AD\bot CM\Rightarrow\Delta AMC\) cân tại A \(\Rightarrow AM=AC\)
Cho tam giác ABC , đường trung tuyến AM . CMR : nếu \(cotB=3.cotC\) thì AM=AC
Gọi AH là đường cao của tam giác ABC (H thuộc BC)
Ta có : \(cotB=\frac{BH}{AH};cotC=\frac{CH}{AH}\) . Theo giả thiết : \(cotB=3cotC\Rightarrow BH=3CH\)
Mà BH + CH = BC\(\Rightarrow BC=4CH\Rightarrow CH=\frac{BC}{4}=\frac{2CM}{4}=\frac{CM}{2}\)
Vậy \(CH=\frac{1}{2}CM\); Ta cũng có : \(BH=BM+MH=2CH+MH=3CH\Rightarrow MH=CH\)
Do đó AH là đường trung trực của CM => AC = AM (đpcm)
AM sao có thể bằng AC đc? Đề có vấn đề j ko bn?
Cho tam giác ABC, đường trung tuyến AM, đường cao AH.
CMR: Nếu \(\cot B=3\cot C\)thì AM = AC.
Cho tam giác ABC, đường trung tuyến AM, đường cao AH.
CMR: Nếu \(\cot B=3\cot C\)thì AM = AC.
CMR nếu tam giác ABC = tam giác A'B'C' thì những đường trung tuyến A'M' và AM của chúng cũng bằng nhau
cho tam giác ABC vẽ trung tuyến AM
CMR: nếu Cot B=3 Cot C thì AM=AC
Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì trung tuyến AM cũng là đường trung trực của cạnh BC;
b) Nếu tam giác ABC có trung tuyến AM đồng thời là đường trung trực của cạnh BC thì tam giác ABC cân tại A.
cho tam giác ABC ,AM là đường trung tuyến
a: cmr nếu A=90độ thì AM=1/2 BC
b:nếu A>90độ thì => AM<1/2DC
C:nếu A<90 độ thì =>AM>1/2 BC
Cho tam giác ABC vuông tại A. Nếu AM là đường trung tuyến thì:
A. A M ⊥ B C .
B. AM = MC.
C. M trùng với đỉnh A.
D. M nằm ở trong tam giác ABC
+ Ta có AM là trung tuyến thì M là trung điểm cạnh BC, nên M ≠ A nên C sai.
+ Tương tự M nằm trên cạnh BC nên M không nằm trong tam giác ABC, nên D sai.
+ A M ⊥ B C khi tam giác ABC là tam giác cân (Theo chứng minh ở câu 6), nên A sai.
Vậy B là đáp án đúng.
Ta chứng minh B đúng như sau:
Trên tia đối của tia MA lấy điểm D sao cho MA = MD
Xét tam giác AMB và tam giác DMC, ta có:
MA = MD (ta dựng)
MB = MC (M là trung điểm BC)
M 1 ^ = M 2 ^


Đáp án B