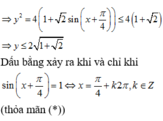lớp 12 : tìm min , max y= căn(1+2sinx)+căn(1+2cosx)

Những câu hỏi liên quan
giải hộ em
a,Tìm min, max: 4x-16 căn x+4y-22 căn y-4 căn xy+36
b, tìm max :B= 6 cẵn+3/2x+4
c, Tìm Min : C=2/1-x+1/x
tìm max(min) của
A=2x^2-5x+1
B=-5x^2+10x-12
C=căn bậc hai của (2x-3) + căn bậc hai của(y-1) SAU ĐÓ + 2015
Tìm Min và Max
f(x) = \(\sqrt{1+2cosx}+\sqrt{1+2sinx}\)
Tìm GTLN và GTNN của hàm số : 1. y = sinx + 2cosx +1 / 2sinx + cosx + 3
2.y= 2sin^2sinx - 3 sinx cosx + cos^2 x
Giải phương trình : 1. 2sin^2 * 2x + sin7x -1 = sinx
2.cos 4x + 12 sin^2 x -1 = 0
với các số thực x,y thỏa mãn:
x-căn(x+6) = căn(y+6)-y.
tìm MIN MAX của P=x+y
Từ bài ra ta có.
\(x+y=\sqrt{x+6}+\sqrt[]{y+6}\)
\(P^2=x+y+12+2.\sqrt{x+6}.\sqrt{y+6}=P+12+2.\sqrt{x+6}.\sqrt{y+6}\)
Mà \(2\sqrt{\left(x+6\right)\left(y+6\right)}\le x+6+y+6=P+12\)
Nên \(P^2\le2P+24\Leftrightarrow P^2-2P+1\le25\)
==>\(\left(P-1\right)^2\le25\Leftrightarrow-5\le P-1\le5\)
Đến đây bạn tự giải tiếp hộ nhé.
Có gì sai sót xin thứ lỗi.
Đúng 0
Bình luận (0)
\(x-\sqrt{x+6}=\sqrt{y+6}-y\)
\(\Leftrightarrow P=x+y=\sqrt{x+6}+\sqrt{y+6}\)
Suy ra \(P^2=x+y+12+2\sqrt{\left(x+6\right)\left(y+6\right)}\le x+y+12+2.\frac{x+y+12}{2}\)
\(\Leftrightarrow P^2\le2P+24\Leftrightarrow P^2-2P-24\le0\Leftrightarrow-4\le P\le6\)
Đúng 1
Bình luận (0)
a )max -13 - căn bậc hai của 2x-13
b) 5-x/3=y+2/4 và x+y=-1
c)tìm x 3/2x+7=5/3x+9
d)C=1,01+1,03+1,05+...+2,09
e)min(1*2)^2+ căn bậc hai của x+1
g) max : -11-căn bậc hai của 9x-18 + căn bậc hai x-2
hơi lộn xôn nhưng cố gắng giúp mik nhé !
Tìm giá trị lớn nhất của hàm số
y
1
+
2
cos
x
+
1
+
2
sin
x
A. B. C. D.
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = 1 + 2 cos x + 1 + 2 sin x
A.![]()
B. ![]()
C.![]()
D. ![]()
Đáp án B
Điều kiện 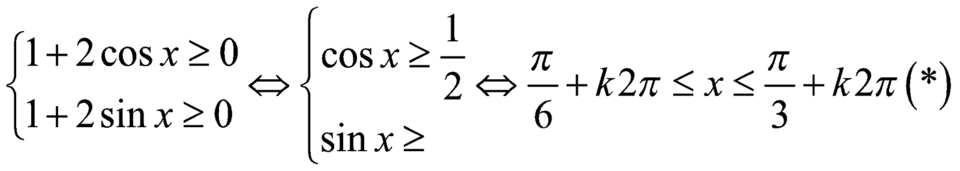
Theo bất đẳng thức BunhiaCopxki: ![]()
![]()
Dấu bằng xảy ra khi và chỉ khi ![]() (thỏa mãn (*))
(thỏa mãn (*))
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của hàm số
y
1
+
2
cos
x
+
1
+
2
sin
x
A.
4
1
+
2
B.
2
1
+
2
C.
2
2
D. ...
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = 1 + 2 cos x + 1 + 2 sin x
A. 4 1 + 2
B. 2 1 + 2
C. 2 2
D. 2
cho các số thực x y thỏa mãn x+y =15. tìm max của A= căn x+ 1 + căn y + 2
\(A^2=\left(\sqrt{x+1}+\sqrt{y+2}\right)^2\le2\left(x+1+y+2\right)=36\)
\(\Rightarrow A\le6\)
\(A_{max}=6\) khi \(\left\{{}\begin{matrix}x=8\\y=7\end{matrix}\right.\)
Đúng 0
Bình luận (0)