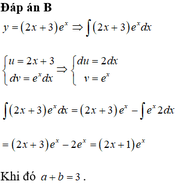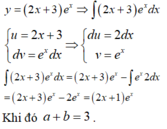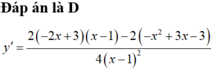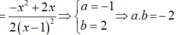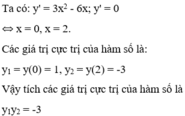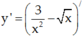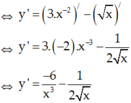Cho hàm số: y=f(x)=3x2 - 1. Khi đó:

Những câu hỏi liên quan
Cho hàm số yf(x) có bảng biến thiên như hình vẽ.Khi đó phương trình f(x) +1m có ba nghiệm thực phân biệt khi và chỉ khi A. 1m2 B.
1
≤
m
≤
2
C.
0
≤
m
≤
1
D. 0m1
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
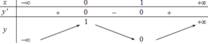
Khi đó phương trình f(x) +1=m có ba nghiệm thực phân biệt khi và chỉ khi
A. 1<m<2
B. 1 ≤ m ≤ 2
C. 0 ≤ m ≤ 1
D. 0<m<1
Biết
F
(
x
)
(
a
x
+
b
)
.
e
x
là nguyên hàm của hàm số
y
(
2
x
+
3
)
.
e
x
. Khi đó a+b là A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Biết F ( x ) = ( a x + b ) . e x là nguyên hàm của hàm số y = ( 2 x + 3 ) . e x . Khi đó a+b là
A. 2
B. 3
C. 4
D. 5
Biết
F
(
x
)
(
a
x
+
b
)
e
x
là nguyên hàm của hàm số
y
(
2
x
+
3
)
e
x
Khi đó a+b là A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Biết F ( x ) = ( a x + b ) e x là nguyên hàm của hàm số y = ( 2 x + 3 ) e x Khi đó a+b là
A. 2
B. 3
C. 4
D. 5
Cho hàm số
y
-
x
3
+
3
x
2
+
m
(m là tham số) có đồ thị (C). Gọi A, B là các điểm cực trị của đồ thị (C). Khi đó, số giá trị của tham số m để diện tích tam giác OAB (O là gốc tọa độ) bằng 1 là: A. 0 B. 2 C. 1 D. 3
Đọc tiếp
Cho hàm số y = - x 3 + 3 x 2 + m (m là tham số) có đồ thị (C). Gọi A, B là các điểm cực trị của đồ thị (C). Khi đó, số giá trị của tham số m để diện tích tam giác OAB (O là gốc tọa độ) bằng 1 là:
A. 0
B. 2
C. 1
D. 3
Đạo hàm của hàm số
y
-
x
2
+
3
x
-
3
2
(
x
-
1
)...
Đọc tiếp
Đạo hàm của hàm số y = - x 2 + 3 x - 3 2 ( x - 1 ) bằng biểu thức có dạng ax 2 + bx 2 ( x - 1 ) 2 . Khi đó a.b bằng
A. -1 .
B. 6 .
C. 4 .
D. -2 .
cho hàm số f(x)=x^2014-2015x^2013+2015x^2012= 2015x^2011+....-2015x+2015. khi đó f(2014)=.....
GIẢI CHI TIẾT NHÉ|
Cho hàm số y = x 3 - 3 x 2 + 1 . Tích các giá trị cực trị của hàm số là
A. 0
B. -3
C. 2
D. 3
Tính đạo hàm của hàm số sau
y
3
x
2
-
x
Đọc tiếp
Tính đạo hàm của hàm số sau y = 3 x 2 - x
![]()
![]()
![]()
![]()
cho hàm số y=f(x)=ax.
a)Biết a=2 tính f(1);f(-2);f(-4).
b)Tìm a biết f(2)=4; vẽ đồ thị hàm số khi a =2;a=–3.
c) Trong các điểm sau điểm nào thuộc đồ thị của hàm số khi a = 2. A ( 1; 4) B (–1; –2) C (–2; 4) D (–2; –4)
a) a = 2
+ y = f(1) = 2.1 = 2
+ y = f(-2) = 2.(-2) = -4
+ y = f(-4) = 2.(-4) = -8
b) f(2) = 4
=> 4 = a.2
=> a = 2
( Vẽ đồ thị hàm số thì bạn tự vẽ được mà :)) Ở đây vẽ hơi khó )
c) Khi a = 2
=> Ta có đồ thị hàm số y = 2x
+ A(1;4)
=> xA = 1 ; yA = 4
Thế vào đồ thị hàm số y = 2x ta có :
4 = 2.1 ( vô lí )
=> A không thuộc đồ thị hàm số y = 2x
+ B = ( -1; -2 )
=> xB = -1 ; yB = -2
Thế vào đồ thị hàm số y = 2x ta có :
-2 = 2(-1) ( đúng )
=> B thuộc đồ thị hàm số y = 2x
+ C(-2; 4)
=> xC = -2 ; yC = 4
Thế vào đồ thị hàm số y = 2x ta có :
4 = 2(-2) ( vô lí )
=> C không thuộc đồ thị hàm số y = 2x
+ D(-2 ; -4 )
=> xD = -2 ; yD = -4
Thế vào đồ thị hàm số y = 2x ta có :
-4 = 2(-2) ( đúng )
=> D thuộc đồ thị hàm số y = 2x