Giải bài hình: Cho tam giác ABC vuông cân tại A . Trên các cạnh góc vuông của tam giác ABC ;lấy D và E sao AD = AE. Qua D vẽ đường thẳng vuông góc vs BE cắt BC tại K. Qua A vẽ đg thẳng vuông góc vs BE cắt BC tại H. C/m HK = HC
Giải bài hình: Cho tam giác ABC vuông cân tại A . Trên các cạnh góc vuông của tam giác ABC ;lấy D và E sao AD = AE. Qua D vẽ đường thẳng vuông góc vs BE cắt BC tại K. Qua A vẽ đg thẳng vuông góc vs BE cắt BC tại H. C/m HK = HC
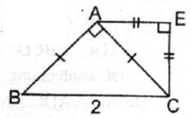
Bài 3: Cho tam giác ABC vuông cân tại A, BC = 2cm. Vẽ về phía ngoài tam giác ACE vuông cân tại E.
Tứ giác AECB là hình gì? Vì sao?
Tính các góc và các cạnh của hình thang AECB.
Lời giải:
a. $BAC$ là tam giác vuông cân tại $A$
$\Rightarrow \widehat{BCA}=45^0$
$ACE$ là tam giác vuông cân tại $E$
$\Rightarrow \widehat{EAC}=45^0$
Do đó: $\widehat{BCA}=\widehat{EAC}$. Mà 2 góc này ở vị trí so le trong nên $AE\parallel BC$. Mà $\widehat{E}=90^0$ nên $AECB$ là hình thang vuông.
-----------------
Tính góc:
Hình thang vuông $AECB$ có $\widehat{E}=90^0$ đương nhiên $\widehat{C}=180^0-\widehat{E}=90^0$
$\widehat{ABC}=45^0$ (do $ABC$ vuông cân tại $A$)
$\widehat{BAE}=\widehhat{BAC}+\widehat{EAC}=90^0+45^0=135^0$
Tính cạnh:
Vì $ABC$ vuông cân tại $A$ nên $AB=AC$
Áp dụng định lý Pitago:
$AB^2+AC^2=BC^2=4$
$AB^2+AB^2=4$
$2AB^2=4\Rightarrow AB=\sqrt{2}$ (cm)
$\Rightarrow AC=\sqrt{2}$ (cm)
Áp dụng định lý Pitago cho tam giác $ACE$ vuông cân tại $E$:
$AE^2+EC^2=AC^2=2$
$2AE^2=2\Rightarrow AE=1$ (cm)
$EC=AE=1$ (cm)
Vậy.........
Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E. Tính các góc và các cạnh của hình thang AECB
∠ E = ∠ (ECB) = 90 0 , ∠ B = 45 0
∠ B + ∠ (EAB) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (EAB) = 180 0 - ∠ B = 180 0 – 45 0 = 135 0
Tam giác ABC vuông tại A. Theo định lí Py-ta-go ta có:
A B 2 + A C 2 = B C 2 mà AB = AC (gt)
⇒ 2 A B 2 = B C 2 = 2 2 = 4
A B 2 = 2 ⇒ AB= √2(cm) ⇒ AC = √2 (cm)
Tam giác AEC vuông tại E. Theo định lí Py-ta-go ta có:
E A 2 + E C 2 = A C 2 , mà EA = EC (gt)
⇒ 2 E A 2 = A C 2 = 2
E A 2 = 1
⇒ EA = 1(cm) ⇒ EC = 1(cm)
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng:
a) HB=HC
b) góc BAH= góc CAK
Bài 2: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng: tam giác ABM= tam giác DCM
Bài 3: Cho tam giác ABC vuông ở A. Trên tia đối AC lấy điểm D sao cho AD= AC
a) chứng minh: tam giác ABC= tam giác ABD
b) Trên tia đối của tia AB lấy điểm M. Chứng minh: tam giác MBD= tam giác MBC
3:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
AB chung
AC=AD
=>ΔABC=ΔABD
b: Xét ΔCBM và ΔDBM có
BM chung
góc CBM=góc DBM
BC=BD
=>ΔCBM=ΔDBM
1 Cho tam giác ABC cân tại A có góc Bac = 50 độ Trên tia đối của tia BC lấy điểm D trên tia đối của tia CB lấy điểm E sao cho BD = BA CE = CA Tính góc Dae
Bài 2 Cho tam giác ABC đều vẽ bên ngoài tam giác các tam giác ABD vuông cân tại B tam giác ACE vuông cân tại C Tính số đo góc nhọn của tam giác ade
Cho tam giác ABC có góc A bằng 80 độ trên các cạnh AB AC BC lấy lần lượt các điểm M N O sao cho MB = BO CO = CN Tính góc MON
Các bạn nhớ vẽ hình hộp mình và giải chi tiết cho mình với
Các bạn nằm ngang giúp mình mình đang cần gấp để mai nộp
Cho tam giác ABC vuông cân tại A , BC = 2cm . Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E
Tính các góc và các cạnh của hình thang AECB
Bài 1:cho tam giác ABC vuông tại A vẽ AH vuông góc BC tại H.Tia phân giác của góc HAC cắt cạnh BC tại D,Elà điểm trên cạnh AB sao cho BE=BH.Chứng minh EH song song với AD
Bài 2:Cho tam giác ABC có BH vuông góc AC tại H và BH=1/2AC và góc BAC =75độ.Chứng minh tam giác ABC cân tại B
khó vãi, giải cả bủi tấu mak 0 ra , mình sr nhá
https://docs.google.com/document/d/1Wuo1vFdubrUg8F8-Ng_f-K8sda_JE_rRM704rtBrI-Q/edit?usp=sharing
Ta có H1+ H2+H3=180
E1+E2=180
mà E1=H1
nên E2=H2+H3
Tong 3 goc trong tam giác: E2+H2+A1=180
(H2+H3)+H2+A1=180
2.H2+H3+A1=180
SUY RA: H2=(180-90-A1):2 *** H3=90 hihi
=45-A1/2
mà A1=90-2A2
thay vào *** ta có H2=45-(90-2.A2)/2=A2
vậy H2=A2 hay EH//AD
Ta có H1+ H2+H3=180
E1+E2=180
mà E1=H1
nên E2=H2+H3
Tong 3 goc trong tam giác: E2+H2+A1=180
(H2+H3)+H2+A1=180
2.H2+H3+A1=180
SUY RA: H2=(180-90-A1):2 *** H3=90 hihi
=45-A1/2
mà A1=90-2A2
thay vào *** ta có H2=45-(90-2.A2)/2=A2
vậy H2=A2 hay EH//AD
Cho ABC vuông cân tại A, Có BC =2cm.Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E. a)Chứng minh rằng AECB là hình thang vuông. b) Tính các góc và các cạnh của hình thang AECB.