Chứng minh rằng: Tổng 3 góc ngoài đỉnh của 1 tam giác thì thằng 3600

Những câu hỏi liên quan
Chứng minh rằng tổng 3 góc ngoài ở 3 đỉnh của 1 tam giác thì bằng 360 độ
Gọi 3 góc ngoài ở 3 đỉnh của 1 tam giác lần lượt là A1;B1;C1 còn A2;B2;C2 là góc trong của tam giác.
Ta có:
A1 + A2 = 180o
B1 + B2 = 180o
C1 + C2 = 180o
=> A1+B1+C1+A2+B2+C2 = 360o
Mà A2 + B2 + C2 = 180o (tổng 3 góc trong của tam giác)
=> A1+B1+C1 = 360o-180o=180o.2 = 360o
Đúng 0
Bình luận (0)
Chứng minh rằng tổng 3 góc ngoài ở ba đỉnh của tam giác thì bằng 360o
Chứng tỏ tổng số đo các góc ngoài ở ba đỉnh của một tam giác bằng 3600.
Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.
Ta có:
$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$
$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=540^0-180^0=360^0$
Đúng 2
Bình luận (0)
Chứng minh rằng tổng ba góc ngoài ở ba đỉnh của một tam giác thì bằng 360º
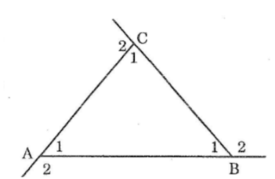
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)
∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)
∠(C1 ) +∠(C2 )=180o(hai góc kề bù)
Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o
⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)
Trong ΔABC, ta có:
∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o
Đúng 0
Bình luận (0)
Chứng minh rằng tổng 3 góc ngoài ở 3 đỉnh của 1 tam giác bằng 360 độ
Chứng minh rằng tổng ba góc ngoài ở đỉnh của một tam giác thì bằng 360o
\(A+A_1+B+B_1+C+C_1=3.180\)
Mà A+B+C=180=> \(A_1+B_1+C_1=360\)
Đúng 0
Bình luận (0)
Câu hỏi tương tự nha ! Kéo xuống là thấy !!!
tích nha
Đúng 0
Bình luận (0)
vì một góc ngoài bằng tổng 2 góc trong cộng lại thì 3 góc ngoài nhân lên bằng 3600(tick nha)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng tổng các góc ngoài của một đa giác có số đo bằng 360 0
Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n-giác bằng 180 0 . Hình n-giác có n đỉnh nên tổng số đo các góc trong và góc ngoài của đa giác bằng n. 180 0 . Mặt khác, ta biết tổng các góc trong của hình n-giác bằng (n – 2). 180 0
Vậy tổng số đo các góc ngoài của hình n-giác là:
n. 180 0 – (n – 2). 180 0 = n. 180 0 – n. 180 0 + 2. 180 0 = 360 0
Đúng 0
Bình luận (0)
CMR trong 1 tứ giác thì tổng các góc ngoài tại mỗi đỉnh bằng 3600
chứng minh rằng tổng 3 góc ngoài ở 3 đỉnh của tam giác = 360 độ
theo tinh chat goc ngoai cua tam giac , ta lan luo co :
goc ngoai cua a=goc b+goc c
goc ngoai cua b=goc a+goc c
goc ngoai cua c=goc a+goc b
cong theo tung ve cua cac dang thuc tren ta duoc:
goc ngoai cua a +goc ngoai cua b+goc ngoai cua c=goc b+gocc+goca+goc c+goca+goc b=2(goc a+goc b+goc c)=2.180 do =360 do
minh lam vay chu trong bai ban ghi goc ngoai cua a la a1 ,goc ngoai cua b la b1, goc ngoai cua c=c1 nhe de cho de lam
Đúng 0
Bình luận (0)
nhầm. Bài này dựa vào tính chất góc trong là ra mế
Đúng 0
Bình luận (0)




















