Thầy cô giúp e bài này với ạ 

Những câu hỏi liên quan
Thầy cô giải giúp e bài này với ạ 
37 distinguish
38 illiteracy
39 energetic
40 disconnected
41 anxiety
42 mysteriously
43 significant
44 frightening
45 repeatedly
46 cancellation
47 disastifying
48 products
49 disagree
50 typicallu
51 socialize
52 vegetarian
53 entrance
54 modernized
55 income
Đúng 1
Bình luận (1)
Thầy cô giúp em giải bài word form này với ạ, e cảm ơn 
1 inconvenience
2 voluntarily
3 industrial
4 break-taking
5 intentively
6 breakdown
7 preferable
8 economical
9 acceleration
10 misunderstanding
11 inhabitant
12 kidnapper
13 foggy
14 shouthern
15 decision
16 entertainment
17 information
18 pronounciation
Đúng 2
Bình luận (1)
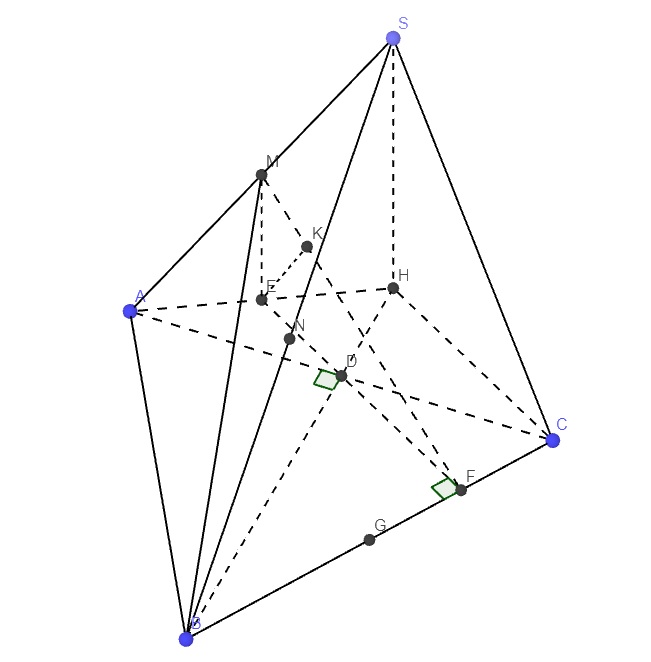
Thầy cô hướng dẫn giúp e bài này ạ, e cảm ơn ạ
Gọi D là trung điểm AC
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AB, qua C kẻ đường thẳng vuông góc AC, chúng cắt nhau tại H
Dễ dàng nhận ra hai tam giác vuông HAC và HAB có cặp cạnh huyền - cạnh góc vuông bằng nhau nên 2 tam giác bằng nhau
\(\Rightarrow HA=HC\Rightarrow H\) nằm trên trung trực AC (do AB=BC)
\(\Rightarrow H,A,D\) thẳng hàng
\(\left\{{}\begin{matrix}CH\perp BC\\SC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SHC\right)\Rightarrow BC\perp SH\)
Tương tự ta có \(AB\perp\left(SHA\right)\Rightarrow AB\perp SH\)
\(\Rightarrow SH\perp\left(ABC\right)\)
Gọi E là trung điểm AH \(\Rightarrow ME\) là đường trung bình tam giác SAH
\(\Rightarrow ME||SH\Rightarrow ME\perp\left(ABC\right)\) đồng thời \(ME=\dfrac{1}{2}SH\)
Gọi G là trung điểm BC \(\Rightarrow AG\perp BC\), từ D kẻ \(DF\perp BC\Rightarrow DF||AG\Rightarrow DF\) là đường trung bình tam giác AGC
\(\Rightarrow DF=\dfrac{1}{2}AG=\dfrac{a\sqrt{3}}{4}\)
AGCH là hình thang (AG song song CH vì cùng vuông góc BC) \(\Rightarrow EF\) là đường trung bình hình thang
\(\Rightarrow EF\perp BC\Rightarrow E,D,F\) thẳng hàng
\(AH=\dfrac{AD}{cos\widehat{DAH}}=\dfrac{AD}{cos\widehat{ABD}}=\dfrac{AD}{cos30^0}=\dfrac{a\sqrt{3}}{3}\)
\(ED=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\) (trung tuyến tam giác vuông)
\(\Rightarrow EF=ED+DF=\dfrac{5a\sqrt{3}}{12}\)
Trong tam giác vuông MEF, từ E kẻ \(EK\perp MF\)
\(\left\{{}\begin{matrix}ME\perp\left(ABC\right)\Rightarrow ME\perp BC\\EF\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(MEF\right)\Rightarrow BC\perp EK\)
\(\Rightarrow EK\perp\left(MBC\right)\Rightarrow EK=d\left(E;\left(MBC\right)\right)\)
\(SB=2NB\Rightarrow d\left(S;\left(MBC\right)\right)=2d\left(N;\left(MBC\right)\right)\)
\(SM=AM\Rightarrow d\left(S;\left(MBC\right)\right)=d\left(A;\left(MBC\right)\right)\)
\(AC=2DC\Rightarrow d\left(A;\left(MBC\right)\right)=2d\left(D;\left(MBC\right)\right)\)
\(\dfrac{EF}{DF}=\dfrac{5}{3}\Rightarrow d\left(E;\left(MBC\right)\right)=\dfrac{5}{3}d\left(D;\left(MBC\right)\right)=\dfrac{5}{3}d\left(N;\left(MBC\right)\right)\)
\(\Rightarrow EK=\dfrac{5}{3}.\dfrac{3a}{7}=\dfrac{5a}{7}\)
\(\dfrac{1}{EK^2}=\dfrac{1}{ME^2}+\dfrac{1}{EF^2}\Rightarrow ME=\dfrac{EF.EK}{\sqrt{EF^2-EK^2}}=5a\)
\(\Rightarrow SH=2ME=10a\)
\(V=\dfrac{1}{3}.10a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{5a^3\sqrt{3}}{6}\)
Đúng 1
Bình luận (0)
Thầy cô và các bạn giúp e bài này ạ . 
Thầy cô giải bài này giúp e vs ạ, thanks
Dạ Em chào Thầy/Cô ạ!
Dạ Thầy/Cô giúp em giải bài này với ạ !
Em xin cảm ơn ạ

1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25
Đúng 1
Bình luận (1)
Thầy cô giúp e với, bài 2 thôi ạ, giúp e với e đang cần gấp 
2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được
Đúng 2
Bình luận (0)
Giúp em giải bài này với thầy cô ơi..
Bài này giải bằng cách bấm máy tính ạ
Thầy cô giúp em bài này với ạ, cảm ơn nhiều 
146 unemployed
147 communicative
148 disqualified
149 widen
150 completely
151 eaten
153 underpaid
154 misbehaved
155 resignation
156 widespread
157 imprisonment
158 underestimated
159 justify
160 single-minded
161 standardized
162 anxiety
163 growth
146 accustomed
Đúng 2
Bình luận (0)