Cho tam giác ABC cạnh AB=4,AC=6,BC=8 gọi M là trung điểm của BC và D là trung điểm của BM .Tính DA

Những câu hỏi liên quan
Cho tam giác ABC cạnh AB=4,AC=6,BC=8 gọi M là trung điểm của BC và D là trung điểm của BM .Tính DA
Cho tam giác ABC nhọn (AB < AC), Gọi D là trung điểm của BC. Trên tia đối của tia Da lấy điểm M sao cho DM = DA a) C/m : AC = BM và AC// BM b) C/m : TAM giác ABM = TAM GIÁC MCA
\(a,\)
Xét \(\triangle ADC\) và \(\triangle MDB\):
\(DA=DM\)
\(DC=DB\)
\(\widehat{ADC}=\widehat{MDB}\)
\(\Rightarrow\Delta ADC=\Delta MDB\left(c.g.c\right)\) \(\left(1\right)\)
\(\left(1\right)\Rightarrow AC=BM\)
\(\Rightarrow\widehat{ACD}=\widehat{MBD}\)
mà hai góc này nằm ở vị trí so le trong
\(\Rightarrow\)\(AC//BM\)
\(b,\)
\(\left(1\right)\Rightarrow\widehat{DAC}=\widehat{DMB}\)
Xét \(\triangle ABM\) và \(\triangle MCA\):
\(AM\) chung
\(BM=AC\)
\(\widehat{DAC}=\widehat{DMB}\)
\(\Rightarrow\Delta ABM=\Delta MCA\left(c.g.c\right)\).
Đúng 1
Bình luận (0)
a: Xét tứ giác ABMC có
D là trung điểm chung của AM và BC
=>ABMC là hình bình hành
=>AC//BM và AC=BM
b: Xét ΔABM và ΔMCA có
AB=MC
BM=CA
AM chung
=>ΔABM=ΔMCA
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (AB AC). Gọi D là trung điểm của BC. Trên tia đối của tia DA lấy điểm M sao cho DM DA.a) Chứng minh AC BM và AC // BM.b) Chứng minh
∆
A
B
M
∆
M
C
A
.
c) Kẻ
A
H
⊥
B
C
,
M
K
⊥
B
C
(
H
,
K
∈
B...
Đọc tiếp
Cho tam giác nhọn ABC (AB < AC). Gọi D là trung điểm của BC. Trên tia đối của tia DA lấy điểm M sao cho DM = DA.
a) Chứng minh AC = BM và AC // BM.
b) Chứng minh ∆ A B M = ∆ M C A .
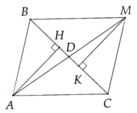
c) Kẻ A H ⊥ B C , M K ⊥ B C ( H , K ∈ B C ) . Chứng minh BK = CH.
d) Chứng minh HM // AK.
Một tam giác ABC có AB=4cm, AC= 6 cm, BC= 8 cm. M là trung điểm của BC. D là trung điểm của BM. Tính AD
Vì M là trung điểm của BC nên:BM=MC=8:2=4 (cm)
mà BD=1:2BM Vậy BD=2(CM)
Vậy AD=8(CM)
Đúng 0
Bình luận (0)
Cho tam giác ABC , gọi D, E,F là trung điểm của các cạnh AB , AC, BC . M,N,P,Q lần lượt là trung điểm của cạnh DA , AE, EF , FD.
a, CM : EF là đường trung bình của tam giác ABC
Xem chi tiết
Bài 1: Cho tam giác ABC(AB<AC), AD là tia phân giác của góc BAC(D∈BC). Trên cạnh AC lấy điểm M sao cho AM=AB
1) Chứng minh △ABD=△AMD
2) Gọi I là giao điểm của AD và BM. Chứng minh I là trung điểm của BM và AI ⊥BM.
3) Gọi K là trung điểm của AM, trên tia đối của tia KB lấy điểm P sao cho KB=KP. Chứng minh MP//AB
1: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC(AB<AC), AD là tia phân giác của góc BAC(D∈BC). Trên cạnh AC lấy điểm M sao cho AM=AB
1) Chứng minh △ABD=△AMD
2) Gọi I là giao điểm của AD và BM. Chứng minh I là trung điểm của BM và AI ⊥BM.
3) Gọi K là trung điểm của AM, trên tia đối của tia KB lấy điểm P sao cho KB=KP. Chứng minh MP//AB
1: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
Đúng 0
Bình luận (0)
giúp tui nha !
Cho tam giác ABC(AB<AC), AD là tia phân giác của góc BAC(D∈BC). Trên cạnh AC lấy điểm M sao cho AM=AB
1) Chứng minh △ABD=△AMD
2) Gọi I là giao điểm của AD và BM. Chứng minh I là trung điểm của BM và AI \perp⊥BM.
3) Gọi K là trung điểm của AM, trên tia đối của tia KB lấy điểm P sao cho KB=KP. Chứng minh MP//AB
1: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn (AB<AC). Gọi D là trung điểm của cạnh BC. Trên tia đối của tia DA lấy E sao cho DA=DE. Kẻ BM vuông góc với AD tại M, CN vuông góc với DE tại N.
a, Cm tam giác ABD= tam giác ECD. Suy ra AB//CE.
b, Cm BM // CN và BM=CN
c, Kẻ AH vuông góc với BD tại H, EK vuông góc với DC tại K. Đoạn AH cắt BM tại O, đoạn EK cắt CN tại I. Cm O,D,I thẳng hàng.
a: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
Do đó: ΔABD=ΔECD
Đúng 0
Bình luận (0)