TL:

Ta có: \(10^{28}+8=100...00\)(\(28\) chữ số \(0\)) \(+8⋮9\) ( Vì \(1+8=9⋮9\))

Vậy\(10^{28}+8⋮9\) thoả mãn bài toán

CHÚC BẠN HỌC TỐT NHÉ.

10²⁸ + 8 chia hết cho 9

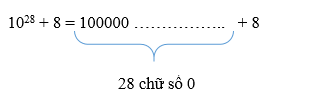
10²⁸ + 8 = 1 + 0 + 0 + ............... + 8 = 9

Mà \(9⋮9\)

\(\Rightarrow10^{28}+8⋮9\)

a 2001^2017 -1 chia hết cho 10

ta có 2001^ 2017 -1^2017 chia hết cho 10 

ta thấy 2 số này có chung số mũ , ta lại có 

2001-1=2000 ( 2000 chia hết cho 10)

ta chứng minh được 2001^2017 -1 chia hết cho 10

còn những câu khác bạn tự làm nha

3⁴ⁿ sẽ có tận cùng bằng 1

(......1) - (.....6) = (......5) chia hết cho 5 (đpcm)

10 chia 3 du 1=> 10^2017 chia 3 du 1

2016 chia het cho 3 => dpcm 

1) đề sai

2) \(A=\left|x-2016\right|+\left|x-2017\right|=\left|x-2016\right|+\left|2017-x\right|\ge\left|x-2016+2017-x\right|=1\)

Dấu "=" xảy ra khi: \(2016\le x\le2017\)

Bài 4:

$A+2=1+2+2^2+2^3+...+2^{11}$

$=(1+2)+(2^2+2^3)+....+(2^{10}+2^{11})$

$=(1+2)+2^2(1+2)+....+2^{10}(1+2)$

$=(1+2)(1+2^2+....+2^{10})$

$=3(1+2^2+...+2^{10})\vdots 3$

Vậy $A+2\vdots 3$ nên $A$ không chia hết cho $3$

Bài 5:

$n^2+n+1=n(n+1)+1$
Vì $n,n+1$ là hai số tự nhiên liên tiếp nên sẽ tồn tại một số chẵn và 1 số lẻ

$\Rightarrow n(n+1)$ chẵn 

$\Rightarrow n^2+n+1=n(n+1)+1$ lẻ (điều phải chứng minh) 

Ta có : 10²⁰¹⁷ = 100....00 ( 2017 chữ số 0 ) 

1000......00 ( 2017 chữ số 0 ) + 2016 = 1000....02017 ( 2013 chữ số 0 ) 

Tổng các chữ số 10.....002017 là :

         1 + 0 + 0 + 0 +......+ 0 + 2 + 0 + 1 + 7 = 13

Mà 13 không chia hết cho 3

=> 10²⁰¹⁷ + 2016 không chia hết cho 3

Ta có : 10²⁰¹⁷ = 100....00 ( 2017 chữ số 0 ) 

1000......00 ( 2017 chữ số 0 ) + 2016 = 1000....02017 ( 2013 chữ số 0 ) 

Tổng các chữ số 10.....002017 là :

         1 + 0 + 0 + 0 +......+ 0 + 2 + 0 + 1 + 7 = 13

Mà 13 không chia hết cho 3

=> 10²⁰¹⁷ + 2016 không chia hết cho 3