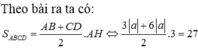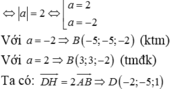cho A(-1 -3) B(1 1) và C(3 -1).tìm tọa độ điểm D để ABCD là hình thang cân biết AB//CD

Những câu hỏi liên quan
cho A(-1 -3) B(1 1) và C(3 -1).tìm tọa độ điểm D để ABCD là hình thang cân biết AB//CD
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân. A. D ( 4;3;0 ) B. D
164
49
;
51
49
;
48
49
C. D
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân.
A. D ( 4;3;0 )
B. D 164 49 ; 51 49 ; 48 49
C. D 1 2 ; 1 3 ; 1 4
D. D ( -4;3;0 )
Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B
Đúng 0
Bình luận (0)
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD2AB và diện tích bằng 28, đỉnh
A
(
-
1
;
-
1
;
0
)
, phương trình đường thẳng chứa cạnh CD là
x
-
2
2
y
+
1
2...
Đọc tiếp
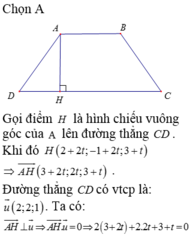
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD=2AB và diện tích bằng 28, đỉnh A ( - 1 ; - 1 ; 0 ) , phương trình đường thẳng chứa cạnh CD là x - 2 2 = y + 1 2 = z - 3 1 . Tìm tọa độ điểm D biết hoành độ điểm B lớn hơn hoành độ điểm A.
![]()
![]()
![]()
![]()
1.Cho hình thang cân ABCD(AB//CD), góc BDC=45o. Gọi O là giao điểm của AC và BD.
a. CM tam giác DOC vuông cân
b. Tính diện tích của hình thang ABCD, biết BD=6cm
2. a. Tìm x của tứ giác ABCD, biết góc A=60 độ, góc C= 90 độ, góc D=63 độ
b. Cho hình thang ABCD(AB//CD). E,F lần lượt là trung điểm AD, BC. Tính độ dài đoạn thẳng EF, biết AB=3cm,CD=9cm
trong mặt phẳng tọa độ oxy cho hình thang cân ABCD( AB song song với CD) có tọa độ đỉnh A(2,-1).giao điểm của 2 đường chéo AC và BD là I(1,2).đường tròn ngoại tiếp tam giác ADI có tâm E(-27/8,-9/8),biết đường thẳng BC qua M(9,-6).tìm B,D , biết B có tung độ nhỏ hơn 3
Bạn giải chi tiết cho mình đc không, mình chưa chứng minh đc
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang ABCD cân. Tìm tọa độ C,D biết A(1;-1); B(3;0) và Sabcd=10
trong mặt phẳng hệ tọa độ Oxy cho hình thang cân ABCD có hai đường chéo BD và AC vuông góc với nhau tại H và AD 2 BC. Gọi M là điểm nằm trên cạnh AB sao cho AB 3 AM N là trung điểm HC. biết B 1 3 đường thẳng HM đi qua T 2 3 đường thẳng DN có phương trình x 2y 2 0 . tìm tọa độ các điểm A,C,D
Bài 1: Cho hình thang cân ABCD ( AB // CD) Gọi E là giao điểm của AC và BD. Chứng minh EA EB.Bài 2: Cho hình thang cân ABCD (AB//CD) có AB3,BCCD13(cm). Kẻ các đường cao AK và BH. a) Chứng minh rằng CHDK. b) Tính độ dài BH.Bài 3: Hình thang cân ABCD (AB//CD) có Cˆ600, DB là tia phân giác của góc D, AB4cm.a) Chứng minh rằng BD vuông góc với BC. b) Tính chu vi hình thang.Bài 4 : Cho hình thang MNPQ (MN là đáy nhỏ) có 2 đường chéo MP và NQ cắt nhau tại O và NMPˆMNQˆA. a) Chứng minh tam giác OMN và...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD ( AB // CD) Gọi E là giao điểm của AC và BD. Chứng minh EA = EB.
Bài 2: Cho hình thang cân ABCD (AB//CD) có AB=3,BC=CD=13(cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Tính độ dài BH.
Bài 3: Hình thang cân ABCD (AB//CD) có Cˆ=600, DB là tia phân giác của góc D, AB=4cm.
a) Chứng minh rằng BD vuông góc với BC.
b) Tính chu vi hình thang.
Bài 4 : Cho hình thang MNPQ (MN là đáy nhỏ) có 2 đường chéo MP và NQ cắt nhau tại O và NMPˆ=MNQˆA.
a) Chứng minh tam giác OMN và OPQ cân tại O.
b) Chứng minh tứ giác MNPQ là hình thang cân.
c) Qua O vẽ đường thẳng EF//QP (E∈MQ,F∈NP). Chứng minh MNFE, FEQP là những hình thang cân.
Bài 5: Cho hình thang cân ABCD (AB//CD, AB < CD). AD cắt BC tại O.
a) Chứng minh rằng ΔOAB cân.
b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng.
c) Qua điểm M thuộc cạnh AC, vẽ đường thẳng song song với CD, cắt BD tại N. Chứng minh rằng MNAB, MNDC là các hình thang cân.
Bài 1:
Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
Suy ra: \(\widehat{BAC}=\widehat{ABD}\)
hay \(\widehat{EAB}=\widehat{EBA}\)
hay ΔEAB cân tại E
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho hình thang ABCD có đáy lớn CD=2AB, điểm C (-1;-1), trung điểm của AD là điểm M(1;-2). Tìm tọa độ điểm B, biết diện tích của tam giác BCD bằng 8, AB=4 và D có hoành độ nguyên dương.
Gọi \(\overrightarrow{n}=\left(a,b\right)\) là vectơ pháp tuyến của CD (\(a^2+b^2\ne0\)
Ta có phương trình CD : \(ax+by+a+b=0\)
\(S_{BCD}=S_{ACD}=8\Rightarrow d\left(A;CD\right)=\frac{2.S}{CD}=2\Rightarrow d\left(M.CD\right)=1\)
\(\Rightarrow\frac{\left|2a-b\right|}{\sqrt{a^2+b^2}}=1\Leftrightarrow3a^2-4ab=0\)\(\rightarrow\begin{cases}a=0;b=1\\a=4;b=3\end{cases}\)\(\rightarrow\begin{cases}CD:y+1=0\\CD:4x+3y+7=0\end{cases}\)
Với \(CD:y+1=0\rightarrow D\left(d;-1\right);CD^2=4.AB^2=64\Leftrightarrow\begin{cases}d=7\\d=-9:L\end{cases}\)
\(D\left(7;-1\right);\overrightarrow{AB}=\frac{1}{2}\overrightarrow{DC}=\left(-4;0\right)\rightarrow B\left(-9;-3\right)\)
Với \(CD:4x+3y+7=0\rightarrow D\left(d;\frac{-4d-7}{3}\right)\rightarrow CD^2=\frac{25\left(d+1\right)^2}{9}=64\) (loại)
Đúng 0
Bình luận (0)