Tìm Sa tạo bởi 2 trục tọa độ và đồ thị hàm số y=3x+5
Cho các hàm số y=2x ; y = 3x + 3 và y= -2x+5
a) Vẽ đồ thị các hàm số trên cùng một hệ trục tọa độ. Tính số đo các góc tạo bởi đồ thị các hàm số trên với trục Ox.
b) Tính diện tích các tam giác tạo bởi mỗi đường thẳng y= 3x + 3 và y= -2x+5 với 2 trục tọa độ
Bài 1: Cho hai hàm số bậc nhất: y= (k+1)x + 3 ; y= (3-2k)x + 1 a)Vẽ đồ thị của hai hàm số trên khi k=2 - Khi k=2 thì ta có hai hàm số : y= 3x+3 và y= -x+1 b) Tìm tọa độ giao điểm của đồ thị hàm số vừa vẽ. c) Tìm góc tạo bởi đường thẳng y= 3x+3 vớt trục Ox ( làm tròn đến phút ) giải giúp mik vs ak!! mik đang cần gấp lắm!!
a)
Thay x=0 vào hàm số y= 3x+3, ta được: y= 3 x 0 + 3 = 3
Thay y=0 vào hàm số y= 3x+3, ta được: 0= 3x+3 => x= -1
Vậy đồ thị hàm số đi qua điểm B(-1;0) và C(0;3)
Thay x=0 vào hàm số y= -x+1, ta được: y= -0 + 1 = 1
Thay y=0 vào hàm số y= -x+1, ta được: 0= -x+1 => x= 1
(Có gì bạn tự vẽ đồ thị nha :<< mình không load hình được sorry bạn nhiều)
b) Hoành độ giao điểm của hai đường thằng y=3x+3 và y=-x+1 :
3x+3 = -x+1
<=> 3x + x = 1 - 3
<=> 4x = -2
<=> x= - \(\dfrac{1}{2}\)
Thay x= - \(\dfrac{1}{2}\) vào hàm số y= -x+1, ta được: y= \(\dfrac{1}{2}\)+1 = \(\dfrac{3}{2}\)
Vậy giao điểm của hai đường thằng có tọa độ (\(-\dfrac{1}{2};\dfrac{3}{2}\))
c) Gọi góc tạo bởi đường thẳng y= 3x+3 là α
OB= \(\left|x_B\right|=\left|-1\right|=1\)
OC= \(\left|y_C\right|=\left|3\right|=3\)
Xét △OBC (O= 90*), có:
\(tan_{\alpha}=\dfrac{OC}{OB}=\dfrac{3}{1}=3\)
=> α= 71*34'
Vậy góc tạo bởi đường thằng y=3x+3 là 71*34'
Cho hàm số y = 3 x + 1 x + 1 1 . Diện tích của tam giác tạo bởi các trục tọa độ và tiếp tuyến của đồ thị của hàm số (1) tại điểm M(-2; 5) là a/b ( phân số tối giản) .Tính a + b.
A: 81
B: 4
C: 85
D: đáp án khác
Bài 2: : Cho hàm số y= -2x +8
a. Vẽ đồ thị hàm số
b. Tính góc tạo bởi đồ thị hàm số với trục ox?
c. Tính khoảng cách từ gốc tọa độ đến đồ thị hàm số?
d. Điểm A(-1; 10 ) có thuộc đồ thị hàm số không?
e. Tính diện tích và chu vi của hình tạo bởi đồ thị hàm số với hai
trục tọa độ?
Cho hàm số bậc nhất y=-2x -5 (d) và y= -x (d') A. Vẽ đồ thị d và d' của 2 hàm số đã cho trêb cùng 1 hệ tọa đọi Oxy B. Tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính) C. Tính góc alpha tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ) D. Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA ( đơn vị đo trên các trục tọa độ là cm)
a) \(\left\{{}\begin{matrix}\left(d\right):y=-2x-5\\\left(d'\right):y=-x\end{matrix}\right.\)
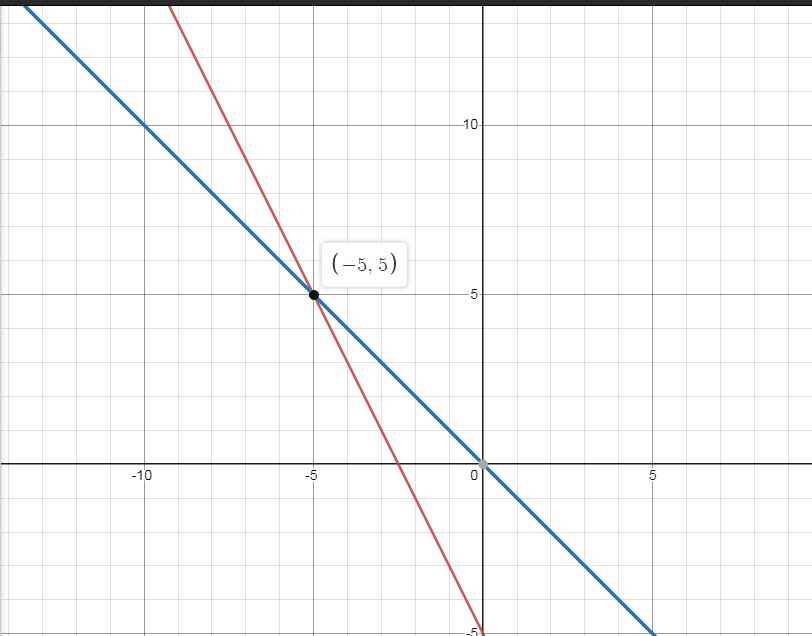
b) \(\left(d\right)\cap\left(d'\right)=M\left(x;y\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
\(\Rightarrow M\left(-5;5\right)\)
c) Gọi \(\widehat{M}=sđ\left(d;d'\right)\)
\(\left(d\right):y=-2x-5\Rightarrow k_1-2\)
\(\left(d'\right):y=-x\Rightarrow k_1-1\)
\(tan\widehat{M}=\left|\dfrac{k_1-k_2}{1+k_1.k_2}\right|=\left|\dfrac{-2+1}{1+\left(-2\right).\left(-1\right)}\right|=\dfrac{1}{3}\)
\(\Rightarrow\widehat{M}\sim18^o\)
d) \(\left(d\right)\cap Oy=A\left(0;y\right)\)
\(\Leftrightarrow y=-2.0-5=-5\)
\(\Rightarrow A\left(0;-5\right)\)
\(OA=\sqrt[]{0^2+\left(-5\right)^2}=5\left(cm\right)\)
\(OM=\sqrt[]{5^2+5^2}=5\sqrt[]{2}\left(cm\right)\)
\(MA=\sqrt[]{5^2+10^2}=5\sqrt[]{5}\left(cm\right)\)
Chu vi \(\Delta MOA:\)
\(C=OA+OB+MA=5+5\sqrt[]{2}+5\sqrt[]{5}=5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)\left(cm\right)\)
\(\Rightarrow p=\dfrac{C}{2}=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}p-OA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5=\dfrac{5\left(\sqrt[]{2}+\sqrt[]{5}-1\right)}{2}\\p-OB=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{2}=\dfrac{5\left(-\sqrt[]{2}+\sqrt[]{5}+1\right)}{2}\\p-MA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{5}=\dfrac{5\left(\sqrt[]{2}-\sqrt[]{5}+1\right)}{2}\end{matrix}\right.\)
\(p\left(p-MA\right)=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}.\dfrac{5\left(1+\sqrt[]{2}-\sqrt[]{5}\right)}{2}\)
\(\Leftrightarrow p\left(p-MA\right)=\dfrac{25\left[\left(1+\sqrt[]{2}\right)^2-5\right]}{4}=\dfrac{25.2\left(\sqrt[]{2}-1\right)}{4}=\dfrac{25\left(\sqrt[]{2}-1\right)}{2}\)
\(\left(p-OA\right)\left(p-OB\right)=\dfrac{25\left[5-\left(\sqrt[]{2}-1\right)^2\right]}{4}\)
\(\Leftrightarrow\left(p-OA\right)\left(p-OB\right)=\dfrac{25.2\left(\sqrt[]{2}+1\right)}{4}=\dfrac{25\left(\sqrt[]{2}+1\right)}{4}\)
Diện tích \(\Delta MOA:\)
\(S=\sqrt[]{p\left(p-OA\right)\left(p-OB\right)\left(p-MA\right)}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25\left(\sqrt[]{2}-1\right)}{2}.\dfrac{25\left(\sqrt[]{2}+1\right)}{2}}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25^2}{2^2}}=\dfrac{25}{2}=12,5\left(cm^2\right)\)
| x | 0 | -5/2 | 1 |
| y=-2x-5 | -5 | 0 | |
| y=-x | 0 | -1 |
*) Đồ thị:
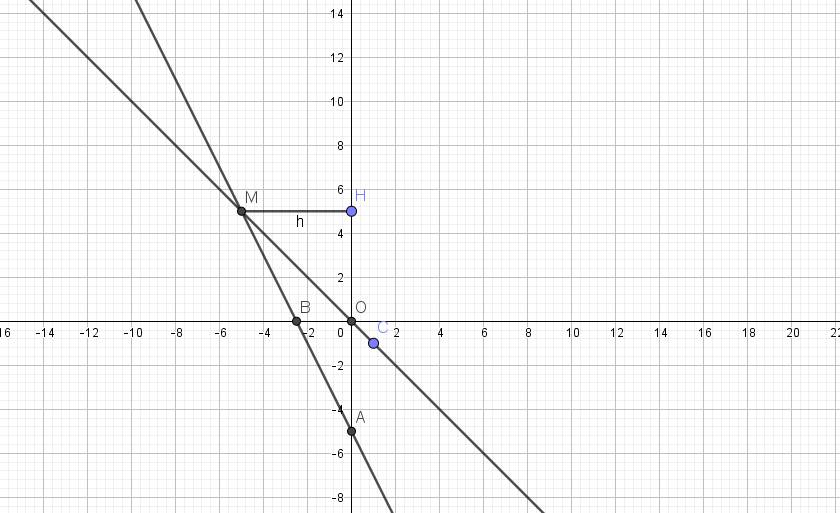
b) Phương trình hoành độ giao điểm của (d) và (d'):
\(-2x-5=-x\)
\(\Leftrightarrow-2x+x=5\)
\(\Leftrightarrow x=-5\) \(\Rightarrow y=-\left(-5\right)=5\)
Vậy tọa độ giao điểm của (d) và (d') là \(M\left(-5;5\right)\)
c) Ta có:
\(tanB=\dfrac{OA}{OB}=\dfrac{-5}{-\dfrac{5}{2}}=2\)
\(\Rightarrow\widehat{B}\simeq63^0\)
Mà góc tạo bởi d với trục hoành là \(\widehat{OBM}\)
\(\Rightarrow\widehat{OBM}\simeq180^0-63^0=117^0\)
d) Ta có:
\(OM^2=5^2+5^2=50\)
\(\Rightarrow OM=5\sqrt{2}\left(cm\right)\)
\(AM^2=5^2+10^2=125\)
\(\Rightarrow AM=5\sqrt{5}\left(cm\right)\)
Chu vi \(\Delta MOA\):
\(5\sqrt{2}+5\sqrt{5}+5=5\left(\sqrt{2}+\sqrt{5}+1\right)\left(cm\right)\)
Diện tích \(\Delta MOA\)
\(S_{MOA}=\dfrac{MH.OA}{2}=\dfrac{5.5}{2}=25\left(cm^2\right)\)
Cho hai hàm số y=(m + 2)x + 2m + 4(với m là một số thực khác –2)
a) Tìm m để diện tích tam giác tạo bởi đồ thị hàm số và hai trục tọa độ bằng 3
PT giao Ox: \(y=0\Leftrightarrow x=\dfrac{-\left(2m+4\right)}{m+2}=-2\Leftrightarrow A\left(-2;0\right)\Leftrightarrow OA=2\)
PT giao Oy: \(x=0\Leftrightarrow y=2m+4\Leftrightarrow B\left(0;2m+4\right)\Leftrightarrow OB=2\left|m+2\right|\)
\(S_{OAB}=3\Leftrightarrow\dfrac{1}{2}OA\cdot OB=3\Leftrightarrow OB=3\\ \Leftrightarrow2\left|m+2\right|=3\Leftrightarrow\left|m+2\right|=\dfrac{3}{2}\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}-2=-\dfrac{1}{2}\\m=-\dfrac{3}{2}-2=-\dfrac{7}{2}\end{matrix}\right.\)
Cho hàm số: y = (2m - 3)x + m - 5.
a) Vẽ đồ thị với m = 6.
b) Chứng minh họ đường thẳng luôn đi qua điểm cố định khi m thay đổi.
c) Tìm m để đồ thị hàm số tạo với 2 trục tọa độ một tam giác vuông cân.
d) tìm m để đồ thị hàm số tạo với trục hoành một góc 45 độ.
e) tìm m để đồ thị hàm số cắt đường thẳng y= 3x-4 tại 1 điểm trên Oy.
f) tìm m để đồ thị hàm số cắt đường thẳng y= 3x-4 tại 1 điểm trên Ox.
NHIỆM VỤ 1: 1. Vẽ đồ thị hàm số y = 3x + 2 và y = 2x +3 trên cùng 1 hệ trục tọa độ 2. Gọi A là giao điểm của đường thẳng y = 3x + 2 với trục Ox; T là một điểm bất kỳ trên đường thẳng y 3x + 2 và T có tung độ dương. Xác định góc tạo bởi tia Ax và AT NHIỆM VỤ 2: 1. Vẽ đồ thị hàm số y= - 3x + 2 và y= - 2x +3 trên cùng 1 hệ trục tọa độ 2. Gọi A là giao điểm của đường thẳng y = -3x + 2 với trục Ox; T là một điểm bất kỳ trên đường thẳng y = -3x + 2 và T có tung độ dương. Xác định góc tạo bởi tia Ax và AT
Bài 4. Cho các hàm số: y =3x và y =-3x +4
1)Vẽ trên cùng hệ trục tọa độ, đồ thị hai hàm số đã cho.
2)Tìm tọa độ giao điểm M của đồ thị hai hàm số trên bằng phép toán.
3)Tính khoảng cách từ O ( gốc tọa độ) đến đường thẳng y =-3x +4.
4)Trong các điểm: C(\(\dfrac{1}{3};3\)) ; D(2;10) điểm nào thuộc, điểm nào không thuộc đồ thịhàm số y= -3x+4. Vì sao?
5)Tìm trên đường thẳng y =-3x+4 điểm có hoành độ bằng x=\(\dfrac{2}{3}\) .
6) Tìm trên đường thẳng y =-3x+4 điểm có tung độ bằng y = -2 .
7) Tìm trên đường thẳng y =-3x +4 điểm M (x;y) sao cho y2+ xy -2x2=0.
8) Tìm trên đường thẳng y =-3x+4 điểm N(x;y) sao cho khoảng cách từ N đến Ox bằng 4 lần khoảng cách từ N đến Oy