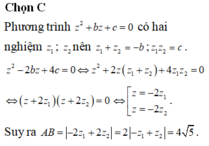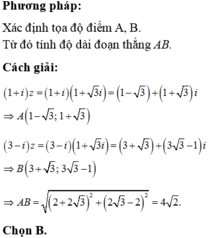Gọi A, B là hai điểm biểu diễn cho các số phức là nghiệm của phương trình \(z^2+2z+3=0\). Tính độ dài đoạn thẳng AB

Những câu hỏi liên quan
Gọi M, N, lần lượt là các điểm biểu diễn hai nghiệm phức của phương trình
z
2
-
4
z
+
9
0
. Tính độ dài đoạn MN. A.
M
N
20
B.
M
N
20
C.
M
N
5
D.
M
N
5
Đọc tiếp
Gọi M, N, lần lượt là các điểm biểu diễn hai nghiệm phức của phương trình z 2 - 4 z + 9 = 0 . Tính độ dài đoạn MN.
A. M N = 20
B. M N = 20
C. M N = 5
D. M N = 5
Trên mặt phẳng tọa độ, gọi A,B là hai điểm biểu diễn hai số phức
z
1
,
z
2
là nghiệm của phương trình
z
2
-
2
z
+
5
0
. Biểu thức
T
O
A
2
+
O
B
2
bằng A. 20 B. ...
Đọc tiếp
Trên mặt phẳng tọa độ, gọi A,B là hai điểm biểu diễn hai số phức z 1 , z 2 là nghiệm của phương trình z 2 - 2 z + 5 = 0 . Biểu thức T = O A 2 + O B 2 bằng
A. 20
B. 2 5
C. 5
D. 10
Cho phương trình
z
2
+
b
z
+
c
0
có hai nghiệm
z
1
;
z
2
thỏa mãn
z
2
-
z
1
4
+
2
i
. Gọi A, B là điểm biểu diễn các nghiệm của phương trình
z...
Đọc tiếp
Cho phương trình z 2 + b z + c = 0 có hai nghiệm z 1 ; z 2 thỏa mãn z 2 - z 1 = 4 + 2 i . Gọi A, B là điểm biểu diễn các nghiệm của phương trình z 2 - 2 b z + 4 c = 0 . Tính độ dài đoạn AB
A. 8 5
B. 2 5
C. 4 5
D. 5
Giả sử
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
2
z
+
5
0
và A, B là các điểm biểu diễn của
z
1
,
z
2
. Tọa độ trung điểm I của đoạn thẳng AB là: A. I(1;1) B. I(-1;0) C. I(0;1)...
Đọc tiếp
Giả sử z 1 , z 2 là hai nghiệm của phương trình z 2 - 2 z + 5 = 0 và A, B là các điểm biểu diễn của z 1 , z 2 . Tọa độ trung điểm I của đoạn thẳng AB là:
A. I(1;1)
B. I(-1;0)
C. I(0;1)
D. I(1;0)
Chọn D.
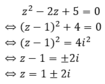
Do đó, tọa độ 2 điểm biểu diễn của z1; z2 là: A(1;2) và B(1;-2)
Do đó tọa độ trung điểm I của đoạn thẳng AB là I(1;0).
Đúng 0
Bình luận (0)
Giả sử z1 , z2 là hai nghiệm của phương trình z2 - 2z + 5 0 và A, B là các điểm biểu diễn của z1 , z2 . Tọa độ trung điểm I của đoạn thẳng AB là: A. I(1;1) B. I(-1;0) C. I(0;1) D. I(1;0)
Đọc tiếp
Giả sử z1 , z2 là hai nghiệm của phương trình z2 - 2z + 5 = 0 và A, B là các điểm biểu diễn của z1 , z2 . Tọa độ trung điểm I của đoạn thẳng AB là:
A. I(1;1)
B. I(-1;0)
C. I(0;1)
D. I(1;0)
Chọn D.
Theo giả thiết ta có:
z2 - 2z + 5 = 0
suy ra: ( z - 1) 2 + 4 = 0 hay z = 1 ± 2i
Tọa độ hai điểm biểu diễn hai số phức z1 và z2là A(1; 2) và B( 1; -2)
Do đó tọa độ trung điểm I của đoạn thẳng AB là I(1; 0).
Đúng 0
Bình luận (0)
Kí hiệu
z
1
,
z
2
là hai nghiệm phức của phương trình
z
2
+
2
i
Gọi M,N là các điểm biểu diễn của các số phức
z
1
,
z
2
Tính
z
2...
Đọc tiếp
Kí hiệu z 1 , z 2 là hai nghiệm phức của phương trình z = 2 + 2 i Gọi M,N là các điểm biểu diễn của các số phức z 1 , z 2 Tính z = 2 + 2 i với O là gốc toạ độ.
A. T = 2 2 .
B. T = 2 2
C. T = 2 2 .
D. T = 2 2
Cho số phức
z
1
+
3
i
. Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB.
Đọc tiếp
Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB.
![]()
![]()
![]()
![]()
Cho số phức
z
1
+
3
i
. Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB
Đọc tiếp
Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các số thực a sao cho phương trình
z
2
+
a
-
2
z
+
2
z
-
3
0
có hai nghiệm phức
z
1
,
z
2
và các điểm biểu diễn của z1, z2 cùng với gốc toạ độ O tạo thành một tam giác đều. Tổng các phần tử của S bằng A....
Đọc tiếp
Gọi S là tập hợp tất cả các số thực a sao cho phương trình z 2 + a - 2 z + 2 z - 3 = 0 có hai nghiệm phức z 1 , z 2 và các điểm biểu diễn của z1, z2 cùng với gốc toạ độ O tạo thành một tam giác đều. Tổng các phần tử của S bằng
A. 12.
B. 11,5
C. 13,5
D. 10.