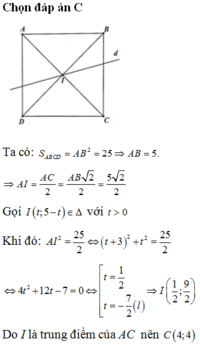Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có tâm \(O\left(\frac{7}{3};\frac{3}{2}\right)\). Điểm \(M\left(6;6\right)\) thuộc cạnh AB và \(N\left(8;-2\right)\) thuộc cạnh BC. Tìm tọa độ các đỉnh của hình vuông

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng
∆
:
x
+
y
-
5
0
và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương.
Đọc tiếp
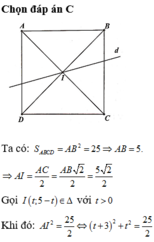
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương.
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng
∆
:
x
+
y
-
5
0
và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương A.
C
9
2
;
-
1
2
B. C(1;8) C. C(4;4)...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương
A. C 9 2 ; - 1 2
B. C(1;8)
C. C(4;4)
D. C(2;2)
 Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A(1; -1) và B(3; 0). Tìm tọa độ điểm D, biết D có tung độ âm.
A.D(0; -1)
B. D( 2; -3)
C. D( 2; -3); D(0; 1)
D. D( -2; -3)
Gọi C= (x, y). Ta có A B → = 2 ; 1 B C → = x − 3 ; y .
Vì ABCD là hình vuông nên ta có A B → ⊥ B C → A B = B C
⇔ 2 x − 3 + 1. y = 0 x − 3 2 + y 2 = 5 ⇔ y = 2 3 − x 5 x − 3 2 = 5 ⇔ y = 2 3 − x x − 3 2 = 1 ⇔ x = 4 y = − 2 hoặc x = 2 y = 2 .
Với C 1 4 ; − 2 ta tính được đỉnh D 1 2 ; − 3 : thỏa mãn.
Với C 2 2 ; 2 ta tính được đỉnh D 2 0 ; 1 : không thỏa mãn.
Chọn B.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho bốn điểm \(A(2;1),B(1;4),C(4;5),D(5;2)\)
a) Chứng minh ABCD là một hình vuông
b) Tìm tọa độ tâm I của hình vuông ABCD
a) Ta có: \(\overrightarrow {AB} = ( - 1;3),\overrightarrow {BC} = (3;1),\overrightarrow {CD} = (1; - 3),\overrightarrow {DA} = ( - 3; - 1)\)
Suy ra \(AB = BC = CD = DA = \sqrt {10} \)
Mặt khác \(\overrightarrow {AB} .\overrightarrow {BC} = ( - 1).3 + 3.1 = 0 \Rightarrow AB \bot BC\)
Vậy ABCD là hình vuông
b) Ta có ABCD là hình vuông, nên tâm I là trung điểm của đoạn thẳng AC
Vậy tọa độ điểm I là \(I(3;3)\)

Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho ba điểm I(1;1) J(-2;2) K(2;-2).Tìm tọa độ các đỉnh của hình vuông ABCD sao cho I là tâm hình vuông, J thuộc cạnh AB và K thuộc cạnh CD.
Trong mặt phẳng tọa độ Oxy, cho 3 điểm có A(-3;-2); B(3;6); C(11;0). Tìm tọa độ điểm D để tứ giác ABCD là hình vuông
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương