Chứng minh rằng với mọi giá trị của tham số m, hàm số
y = x3 – mx2 – 2x + 1
luôn luôn có một điểm cực đại và một điểm cực tiểu.
Những câu hỏi liên quan
Chứng minh rằng với mọi giá trị của tham số m, hàm số y = x 3 - m x 2 - 2 x + 1 luôn luôn có một cực đại và một điểm cực tiểu.
TXĐ: D = R
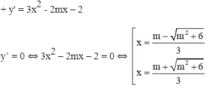
+ y’’ = 6x – 2m.
⇒ 
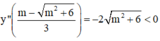
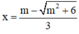là một điểm cực đại của hàm số.
⇒ 
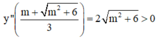
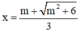là một điểm cực tiểu của hàm số.
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi giá trị của tham số m, hàm số y = x3 – mx2 – 2x + 1 luôn luôn có một điểm cực đại và một điểm cực tiểu.
y= x3-mx2-2x+1
y'=3x^2-2mx-2
PT y'=3x^2-2mx-2=0 có delta'=m^2+6>0 với mọi m
nên có 2 nghiệm phân biệt.
vậy hs có 1 cực đại và 1 cực tiểu
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi giá trị của tham số \(m\), hàm số \(y=x^3-mx^2-2x+1\)
luôn luôn có một điểm cực đại và một điểm cực tiểu
y’ = 3x2 – 2mx – 2 , ∆’ = m2 + 6 > 0 nên y’ = 0 có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.
Đúng 0
Bình luận (1)
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
3
+
m
x
2
+
7
x
+
3
có đường thẳng đi qua điểm cực đại và điểm cực tiểu vuông góc với đường thẳng có phương trình :
y...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 + m x 2 + 7 x + 3 có đường thẳng đi qua điểm cực đại và điểm cực tiểu vuông góc với đường thẳng có phương trình : y = 3 x ( d )
A. m = ± 45 2
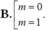
C. m = 2
D. m = ± 47 2
Chọn A
[Phương pháp trắc nghiệm]
y ' = 3 x 2 + 2 m x + 7
Bấm máy tính
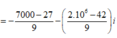
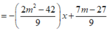
Đường thẳng đi qua 2 điểm cực trị là
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của m để hàm số
y
1
3
x
3
-
m
x
2
+
m
+
2
x
có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương. A.
m
∈
2...
Đọc tiếp
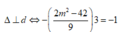
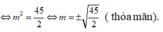
Tìm tất cả các giá trị của m để hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương.
A. m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
B. m ∈ 2 - 2 7 3 ; 2 + 2 7 3
C. m ∈ - 1 ; 2
D. m ∈ - ∞ ; - 1 ∪ 2 ; + ∞
Để đồ thị hàm số có 2 điểm cực trị thì
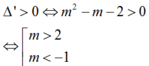
Khi đó, do a = 1 3 > 0 nên hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương . Đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất là x = 0 1 và hai cực trị x 1 ; x 2 x 1 < x 1 thỏa mãn: 0 < x 1 < x 2 2
Ta có:
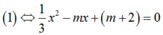
hoặc là vô nghiệm hoặc là có nghiệm kép x = 0
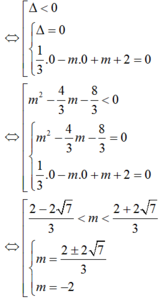
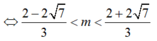
Kết hợp điều kiện ta có:
m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
Chọn: A
Đúng 0
Bình luận (0)
Với giá trị nào của m, đồ thị hàm số
y
x
3
–
m
x
2
+
3
(
m
2
-
1
)
x
–
m
3
+
m
có điểm cực đại B, điểm cực tiểu C thỏa mãn OC 3OB, với O là gốc tọa độ? A. m 2 hoặc
m
1...
Đọc tiếp
Với giá trị nào của m, đồ thị hàm số y = x 3 – m x 2 + 3 ( m 2 - 1 ) x – m 3 + m có điểm cực đại B, điểm cực tiểu C thỏa mãn OC = 3OB, với O là gốc tọa độ?
A. m = 2 hoặc m = 1 2
B. m = 2
C. m = 1 2
D. m = - 1 2 hoặc m = 1 2
Chọn A
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 ) .
Hàm số có hai cực trị => y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=> ( 3 m ) 2 - 3 . 3 ( m 2 - 1 ) > 0 <=> 9 > 0 đúng với mọi m. Ta có điểm cực đại là B(m - 1; -2m + 2) và cực tiểu là C(m + 1; -2m - 2)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của m để đồ thị hàm số
y
m
2
-
1
x
4
+
m
x
2
+
m
-
2
ch...
Đọc tiếp
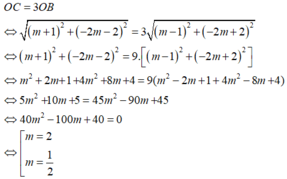
Tìm tất cả các giá trị của m để đồ thị hàm số y = m 2 - 1 x 4 + m x 2 + m - 2 chỉ có một điểm cực đại và không có điểm cực tiểu
A. - 1 , 5 < m ⩽ 0 .
B. m ⩽ - 1
C. - 1 ⩽ m ⩽ 0
D. - 1 < m < 0 , 5
Tìm tất cả các giá trị của m để đồ thị hàm số y
(
m
2
-
1
)
x
4
+
m
x
2
+
m
-
2
chỉ có một điểm cực đại và không có điểm cực tiểu. A. -1,5 m
≤
0 B. m
≤
1 C. -1
≤
m
≤...
Đọc tiếp
Tìm tất cả các giá trị của m để đồ thị hàm số y = ( m 2 - 1 ) x 4 + m x 2 + m - 2 chỉ có một điểm cực đại và không có điểm cực tiểu.
A. -1,5 < m ≤ 0
B. m ≤ 1
C. -1 ≤ m ≤ 0
D. -1 < m < 0,5
Chọn C.
Tập xác định: D = ℝ
Xét 
Với m = 1, hàm số đã cho trở thành: 
Hàm số này đạt cực tiểu tại điểm A(0;-1) nên không thỏa mãn yêu cầu bài toán.
Với m = -1, hàm số đã cho trở thành: 
Hàm số này đạt cực đại tại điểm B(0;-3) nên thỏa mãn yêu cầu bài toán.
Xét m
≠
±
1 ta có 
Xét y' = 0 
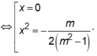
Với m = 0 phương trình y' = 0 có nghiệm bồi 3 và 
nên hàm số đạt cực đại tại điểm C(0;-1) nên thỏa mãn yêu cầu bào toán.
Với m ≠ 0 hàm số đã cho chỉ có một điểm cực đại và không có điểm cực tiểu khi và chỉ khi
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
2
+
m
x
+
m
, điểm A(1;3) và hai điểm cực đại, cực tiểu thẳng hàng ứng với các giá trị của tham số m bằng
A
.
m
5
2
B
.
m
2
C
.
...
Đọc tiếp
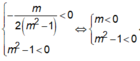
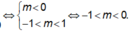
Cho hàm số y = x 3 - 3 x 2 + m x + m , điểm A(1;3) và hai điểm cực đại, cực tiểu thẳng hàng ứng với các giá trị của tham số m bằng
A . m = 5 2
B . m = 2
C . m = 1 2
D . m = 3
