TXĐ: D = R
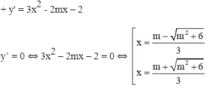
+ y’’ = 6x – 2m.
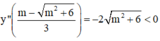
⇒ 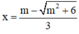 là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.
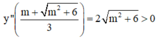
⇒ 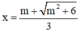 là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.
TXĐ: D = R
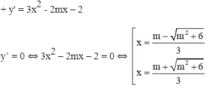
+ y’’ = 6x – 2m.
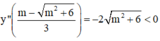
⇒ 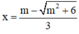 là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.
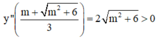
⇒ 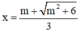 là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Cho hàm số y=x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. m= -1/2
B. m= 1/2
C. m=2
D. m=1
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1). Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
Có bao nhiêu giá trị nguyên của tham số m để điểm M(2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 (C) một tam giác có diện tích nhỏ nhất
A. 0
B. 1
C. 2
D. Không tồn tại
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x 4 + 2 ( m - 1 ) x 2 + 2 có hai điểm cực tiểu và một điểm cực đại
A. m<0
B. 0<m<1
C. m>2
D. 1<m<2
Tìm tất cả các giá trị thực của tham số m để điểm M( 2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y= 2x3-3( 2m+ 1) x2+ 6m( m+1) x+1 (C) một tam giác có diện tích nhỏ nhất.
A. -1
B. 0
C. 1
D. 2
Tìm tất cả các giá trị thực của tham số m để điểm M ( 2 m 3 ; m ) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 một tam giác có diện tích nhỏ nhất
A. m = 2
B. m = 0
C. m = 1
D. m = -1
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn