HELP ME mình sắp thi rồi
giải bóng đã nữ đông nam á tại tp HCM có 8 đội tham gia trong đó có VN và thái lan. các đội bóng đc xếp ngẫu nhiên thành 2 bảng A và B mỗi bảng 4 đội. tính xác suất để 2 đội VN và TL nằm ở 2 bảng khác nhau
Giải bóng đá Đông Nam Á có 8 đội bóng của 8 quốc gia tham dự, trong số đó có 4 đội: Việt Nam, Lào, Thái Lan và Myanma. Ban tổ chức bốc thăm ngẫu nhiên chia 8 đội thành hai bảng A, B và mỗi bẳng có 4 đội thi đấu còng loại. Tính xác suất để hai đội Lào và Myanma phải gặp nhau ở vòng loại, biết rằng Việt Nam và Thái Lan là hai đội hạt giống nên không cùng thuộc một bảng.
A. 3/5
B. 3/7
C. 2/5
D. 2/7
Tại SEA Games 2019, môn bóng chuyền nam có 8 đội bóng tham dự, trong đó có hai đội Việt Nam và Thái Lan. Các đội bóng được chia ngẫu nhiên thành hai bảng có số đội bóng bằng nhau. Xác suất để hai đội Việt Nam và Thái Lan nằm ở hai bảng khác nhau bằng:
A . 3 7
B . 4 7
C . 3 14
D . 11 14
Chọn B
Số phần tử không gian mẫu là số cách chia 8 đội bóng vào hai bảng sao cho mỗi bảng có 4 đội
![]()
Gọi A là biến cố thỏa mãn yêu cầu bài toán.
Ta có: ![]()
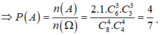
1. Giải bóng chuyền VTV Cúp gồm 12 đội bóng tham dự, trong đó có 9 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C mỗi bảng 4 đội. Tính xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau.
2. Có 11 chiếc thẻ được đánh số từ 1 đến 11, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn.
1. Không gian mẫu: \(C_{12}^4C_8^4C_4^4\)
Xếp 3 đội Việt Nam vào 3 bảng: \(3!=6\) cách
Còn 9 đội nước ngoài, có \(C_9^3C_6^3C_3^3\) cách xếp
Xác suất: \(P=\dfrac{6.C_9^3C_6^3C_3^3}{C_{12}^4C_8^4C_4^4}=...\)
2.
Không gian mẫu: \(C_{11}^2\)
Tích 2 số chẵn khi có ít nhất 1 số chẵn
Số cách chọn 2 thẻ đều lẻ: \(C_6^2\)
Số cách chọn ít nhất 1 thẻ chẵn: \(C_{11}^2-C_6^2\)
Xác suất: \(P=\dfrac{C_{11}^2-C_6^2}{C_{11}^2}=...\)
Giải bóng chuyền VTV Cup gồm 9 đội bóng tham dự, trong đó có 6 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C và mỗi bảng có 3 đội. Tính xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau.
A. 3 56 .
B. 19 28 .
C. 9 28 .
D. 53 56 .
Đáp án C
Cách chia 9 đội ra thành 3 bảng là:
C 9 3 C 6 3 C 3 3 = 1680
Cách chia 3 đội bóng của Việt Nam ở 3 bảng khác nhau là: C 3 1 C 6 2 C 2 1 C 4 2 = 540
⇒ p = 540 1680 = 9 28
Giải bóng chuyền VTV Cup gồm 9 đội bóng tham dự, trong đó có 6 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C và mỗi bảng có 3 đội. Tính xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau
A. 3 56
B. 19 28
C. 9 28
D. 53 56
Đáp án C
Cách chia 9 đội ra thành 3 bảng là: C 9 3 C 6 3 C 3 3 = 1680
Cách chia 3 đội bóng của Việt Nam ở 3 bảng khác nhau là C 3 1 C 6 2 C 2 1 C 4 2 = 540
=> p = 540 1680 = 9 28
Giải bóng chuyền VTV Cup gồm 9 đội bóng tham dự, trong đó có 6 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C và mỗi bảng có 3 đội. Tính xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau
A. 3 56
B. 19 28
C. 9 28
D. 53 56
Đáp án C
Cách chia 9 đội ra thành 3 bảng là
![]()
Cách chia 3 đội bóng của Việt Nam ở 3 bảng khác nhau là
![]()
⇒ p = 540 1680 = 9 28
Giải bóng chuyền VTV Cup gồm 12 đội tham dự trong đó có 9 đội bóng nước ngoài, 3 đội bóng của Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C mỗi bảng có 4 đội. Tính xác suất để 3 đội Việt Nam ở 3 bảng khác nhau.
A. 16 55
B. 133 165
C. 32 165
D. 39 65
Đáp án A.
Không gian mẫu là số cách chia tùy ý 12 đội thành 3 bảng.
Suy ra số phần tử của không gian mẫu là n Ω = C 12 4 . C 8 4 . C 4 4 .
Gọi X là biến cố “3 đội bóng của Việt Nam ở 3 bảng khác nhau”
Bước 1: Xếp 3 đội Việt Nam ở 3 bảng khác nhau nên có 3! cách.
Bước 2: Xếp 6 đội còn lại vào 3 bảng A, B, C này có C 9 3 . C 6 3 . C 3 3 .
Suy ra số phần tử của biến cố X là n X = 3 ! . C 9 3 . C 6 3 . C 3 3 .
Vậy xác suất cần tính là P = n X n Ω = 3 ! . C 9 3 . C 6 3 . C 3 3 C 12 4 . C 8 4 . C 4 4 = 16 55 .
Giải bóng chuyền VTV Cup gồm 12 đội tham dự trong đó có 9 đội bóng nước ngoài, 3 đội bóng của Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C mỗi bảng có 4 đội. Tính xác suất để 3 đội Việt Nam ở 3 bảng khác nhau.
A. 16 55
B. 133 165
C. 32 165
D. 39 65
Đáp án A.
Không gian mẫu là số cách chia tùy ý 12 đội thành 3 bảng.
Suy ra số phần tử của không gian mẫu là n Ω = C 12 4 . C 8 4 . C 4 4 .
Gọi X là biến cố “3 đội bóng của Việt Nam ở 3 bảng khác nhau”
Bước 1: Xếp 3 đội Việt Nam ở 3 bảng khác nhau nên có 3! cách.
Bước 2: Xếp 6 đội còn lại vào 3 bảng A, B, C này có C 9 3 . C 6 3 . C 3 3 .
Suy ra số phần tử của biến cố X là n X = 3 ! . C 9 3 . C 6 3 . C 3 3 .
Vậy xác suất cần tính là P = n X n Ω = 3 ! . C 9 3 . C 6 3 . C 3 3 C 12 4 . C 8 4 . C 4 4 = 16 55 .
Giải bóng truyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của Việt Nam nằm trong hai bảng khác nhau bằng
A. 2 7
B. 5 7
C. 3 7
D. 4 7
Số cách chia 8 đội thành 2 bảng là:
![]()
Gọi A là biến cố: “Hai đội của Việt Nam được xếp vào 2 bảng khác nhau”.
Số các chia 2 đội của Việt Nam vào 2 đội là:
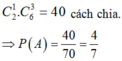
Chọn D.