mn giúp em câu c) với ạ

Những câu hỏi liên quan
Giúp em với mn, câu c thôi ạ. Giải chi tiết (ko tắt) hộ em với ạ

a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
Đúng 1
Bình luận (0)
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
Đúng 0
Bình luận (0)
giúp em bài 3 với ạ trừ câu c,e,j ạ ,em cảm ơn,em đang vội mong mn giúp đỡ
Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)
Đúng 2
Bình luận (2)
Bài 3:
a)3xy-12x2+24xy2=3x(y-4x+8y2)
b)5x3y-30x2y+45xy=5xy(x2-6x+9)=5xy(x-6x+32)=5xy(x-3)2
d)x(x+y)-12x-12y=x(x+y)-(12x+12y)=x(x+y)-12(x+y)=(x+y)(x-12)
f)10x2(x-y)-8xy(x-y)=(x-y)(10x2-8xy)
g)(x-2)3+3x2-6x=(x-2)3+(3x2-6x)=(x-2)3+3x(x-2)=(x-2)[(x-2)+3x]=(x-2)(x-2+3x)=(x-2)(4x-2)
h)x2+15x2y-3xy-5x3=(x2-3xy)+(15x2y-5x3)=x(x-3y)+5x2(3y-x)=x(x-3y)-5x2(x-3y)=(x-3y)(x-5x2)
i)x2-2x-8+4x=(x2-2x)+(4x-8)=x(x-2)+4(x-2)=(x-2)(x+4)
k)4x2-9x-9=4x2+3x-12x-9=(4x2+3x)-(12x+9)=x(4x+3)-3(4x+3)=(4x+3)(x-3)
l)x2-y2+10x+25=(x2+10x+25)-y2=(x2+10x+52)-y2=(x+5)2-y2=[(x+5)+y][(x+5)-y]=(x+5+y)(x+5-y)
m)x2-4y2+24y-36=x2-(4y2-24y+36)=x2-[(2y)2-24y+62]=x2-(2y-6)2=[x+(2y-6)][x-(2y-6)]=(x+2y-6)(x-2y+6)
n)(không biết làm)
Đúng 0
Bình luận (0)
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
mn giúp em câu c và d với ạ!!

$A=x-3\sqrt{x}+1=(x-3\sqrt{x}+\frac{9}{4})-\frac{5}{4}$
$=(\sqrt{x}-\frac{3}{2})^2-\frac{5}{4}$
$\geq \frac{-5}{4}$
Vậy $A_{\min}=-\frac{5}{4}$. Giá trị này đạt tại $\sqrt{x}-\frac{3}{2}=0\Leftrightarrow x=\frac{9}{4}$
----------------
$B=\frac{3\sqrt{x}-1}{\sqrt{x}+2}=3-\frac{5}{\sqrt{x}+2}$
Vì $\sqrt{x}\geq 0$ nên $\sqrt{x}+2\geq 2$
$\Rightarrow \frac{5}{\sqrt{x}+2}\leq \frac{5}{2}$
$\Rightarrow B\geq 3-\frac{5}{2}=\frac{1}{2}$
Vậy $B_{\min}=\frac{1}{2}$ khi $x=0$
Đúng 1
Bình luận (0)
$C=\frac{\sqrt{x}(\sqrt{x}+3)-3(\sqrt{x}+3)+19}{\sqrt{x}+3}$
$=\sqrt{x}-3+\frac{19}{\sqrt{x}+3}$
$=(\sqrt{x}+3)+\frac{19}{\sqrt{x}+3}-6$
$\geq 2\sqrt{19}-6$ theo BĐT Cô-si
Dấu "=" xảy ra khi $(\sqrt{x}+3)^2=19\Leftrightarrow x=28-6\sqrt{19}$
Đúng 1
Bình luận (0)
$D=\frac{\sqrt{x}(\sqrt{x}-1)-2(\sqrt{x}-1)+1}{\sqrt{x}-1}$
$=\sqrt{x}-2+\frac{1}{\sqrt{x}-1}$
$=(\sqrt{x}-1)+\frac{1}{\sqrt{x}-1}-1$
$\geq 2-1=1$ theo BĐT Cô-si
Vậy $D_{\min}=1$. Dấu "=" xảy ra khi $(\sqrt{x}-1)^2=1$
$\Leftrightarrow x=4$
Đúng 1
Bình luận (0)
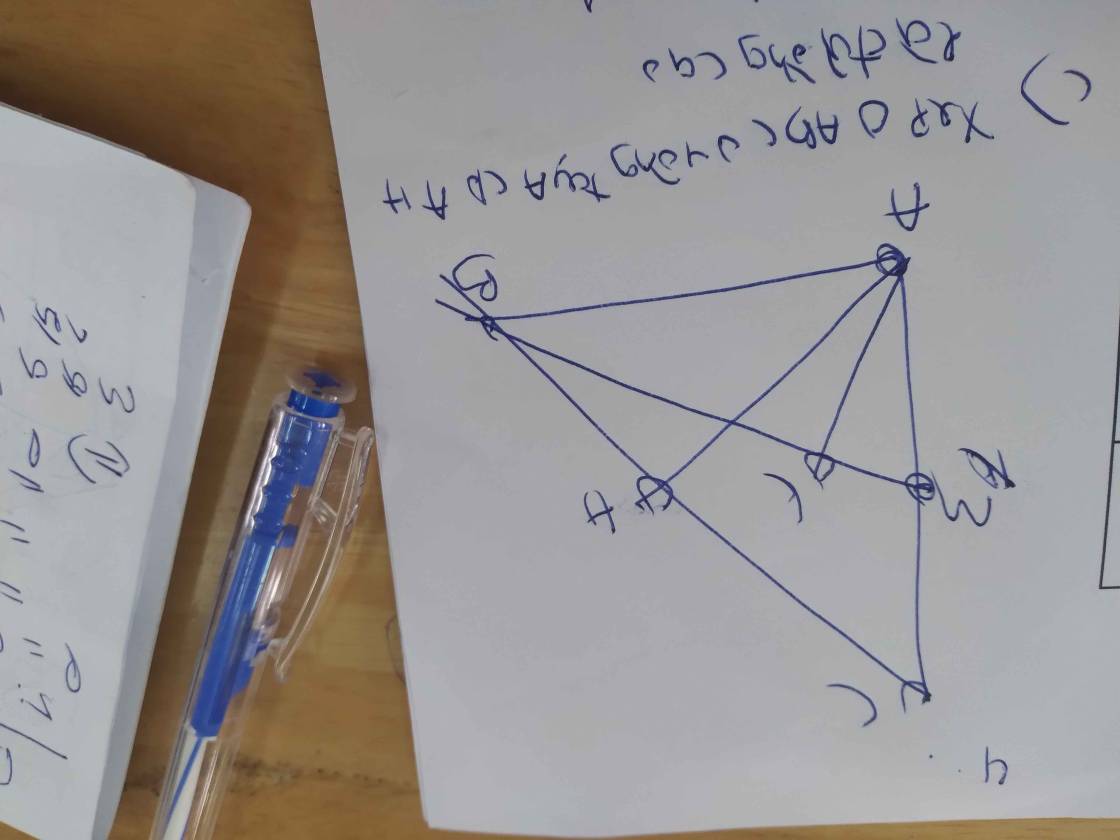
xin lỗi vì đã lm phiền mn ạ, giải hộ em với, em lm hết a với b rồi nên a chị nào giúp em câu c và d với ạ, đc sử dụng dữ kiện của câu trên nhé. GT ( đề bài ) ở bên phải hình vẽ ạ. HTC là hình thag cân ạ, còn cái (n) trong GT là cắt >< Mong mn giúp e ạ
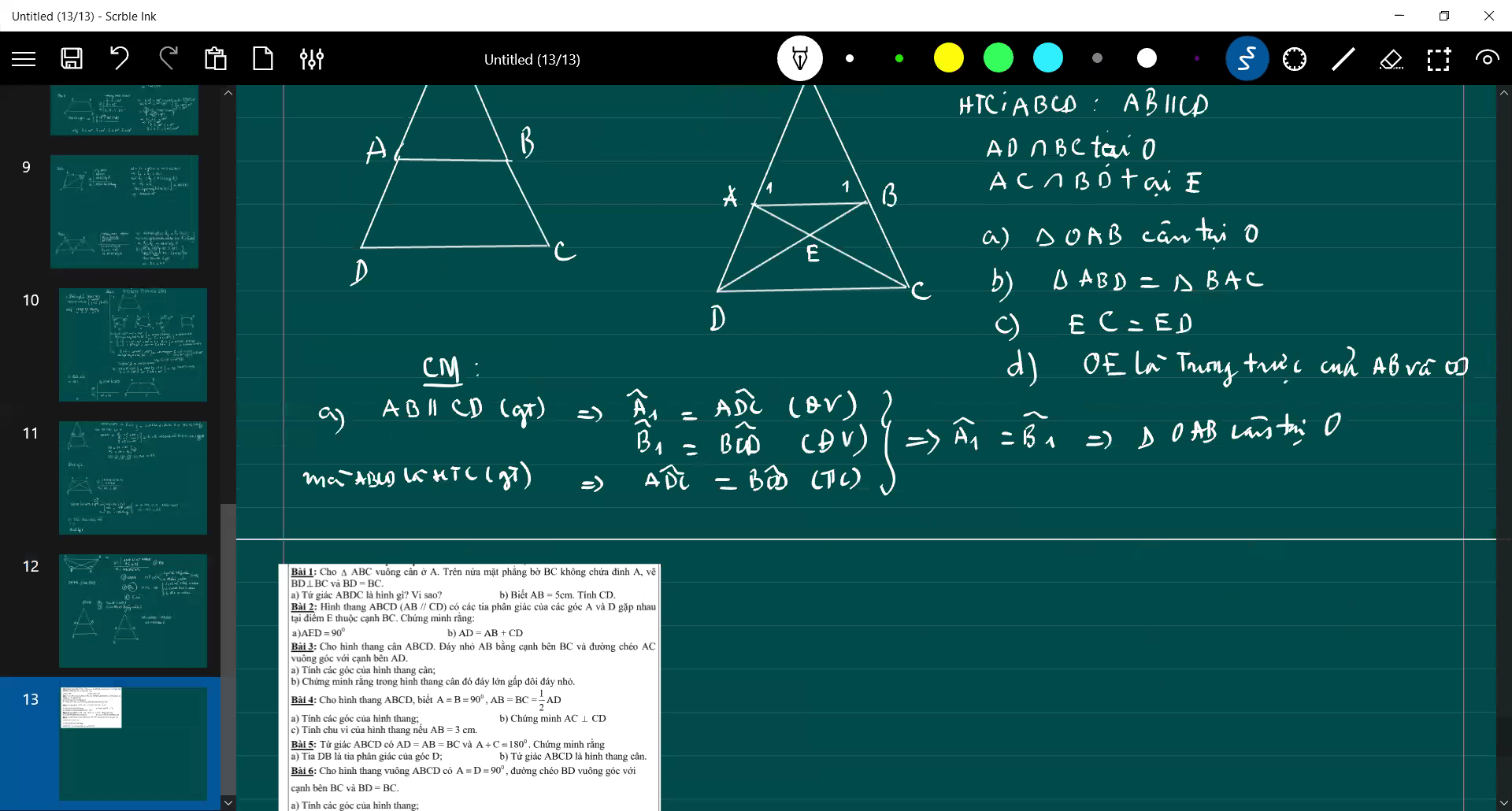
có j thắc mắc thì mn cứ hỏi ạ, em cần trc sáng mai nhé!? ><
Đúng 0
Bình luận (0)
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
Đúng 0
Bình luận (0)
mn giúp em câu c bài hình với bài 5 nhé ạ. Em cảm ơn trước 
Mn giúp em với ạ em cần gấp mai đi học ạ em cảm ơn giúp em câu 1 ạ
\(=>Qthu1=0,2.340000=68000J\)
\(=>Qthu2=2100.0,2.20=8400J\)
\(=>Qtoa=2.4200.25=210000J\)
\(=>Qthu1+Qthu2< Qtoa\)=>đá nóng chảy hoàn toàn
\(=>0,2.2100.20+0,2.340000+0,2.4200.tcb=2.4200\left(25-tcb\right)\)
\(=>tcb=14,5^oC\)
Đúng 3
Bình luận (1)
Mn ơi giúp em câu 6 với ạ, em đang cần gấp
Mong mn giúp đỡ em^^ 
Mn ơi, giúp em với ạ. Always là gì vậy ạ? Em quên rồi nên nhờ mn giúp ạ. Đây là câu hỏi lớp 5 nhé ạ. Cảm ơn mn rất nhiều ạ!
Xem thêm câu trả lời