Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\)

nên \(AB=\dfrac{3}{4}\cdot AC=\dfrac{3}{4}\cdot16=12\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(AB^2+AC^2=BC^2\)

\(\Leftrightarrow BC^2=12^2+16^2=400\)

hay BC=20(cm)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{12^2}{20}=\dfrac{144}{20}=7,2\left(cm\right)\\CH=\dfrac{16^2}{20}=\dfrac{256}{20}=12,8\left(cm\right)\end{matrix}\right.\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=25^2+75=700\)

hay \(BC=10\sqrt{7}\left(cm\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AC^2=CH\cdot BC\)

\(\Leftrightarrow CH=\dfrac{75}{10\sqrt{7}}\)

hay \(CH=\dfrac{15\sqrt{7}}{14}\left(cm\right)\)

tu ve hinh :

a, xet tamgiac AHB va tamgiac AHD co : AH chung

goc AHB =goc AHD = 90^o do AH | BD (gt) 

AB = AD (gt)

=>   tamgiac AHB = tamgiac AHD  (ch - cgv)         (1)

b,  (1) => goc BAE = goc EAD (dn)

xet tamgiac BAE va tamgiac DAE co : AE chung

BA = AD (gt)

=>  xet tamgiac AHB = tamgiac AHD  (c - g - c)

=> EB = ED (dn)

=> tamgiac EBD can tai E (dn)

vay_

Đề sai rồi bạn ơi!!

a: Xét ΔABH vuông tại H và ΔADH vuông tại H có

AB=AD

AH chung

=>ΔABH=ΔADH

b: Xét ΔBAE và ΔDAE co

AB=AD

góc BAE=góc DAE
AE chung

=>ΔBAE=ΔDAE

=>EB=ED

=>ΔEBD cân tại E

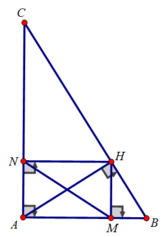
a) Xét tam giác ABC vuông tại A, đường cao AH có:

B C 2 = A B 2 + A C 2 = 25 ⇒ BC = 5(cm)

AB2 = BH.BC ⇒ BH = AB2/BC = 9/5 = 1,8(cm)

BH + CH = BC⇒ CH = BC - BH = 5 - 1,8 = 3,2 (cm)

A H 2 = BH.CH ⇒ AH = B H . C H = 1 , 8 . 3 , 2 = 2,4 (cm)

Xét tứ giác AMHN có:

∠(MAN) = ∠(ANH) = ∠(AMH) = 90 0

⇒ Tứ giác AMHN là hình chữ nhật

⇒ MN = AH = 2,4 (cm)

vẽ hình giùm mình với

Không biết vẽ .

tao chịu mày thế thì mày hỏi làm cái đéo gì hả ôn con