cho hình chóp tứ giác S.ABCD có đáy là hình vuông tâm O. SB tạo với đáy một góc \(30^o\). Tính khoảng cách từ O đến mp(SAD)

Những câu hỏi liên quan
cho hình chóp tứ giác S.ABCD có ABCD là hình vuông tâm O. SB tạo với đáy một góc 30 o . Tính khoảng cách từ O đến mp(SAD)
cho hình chóp tứ giác đều S.ABCD có ABCD là hình vuông tâm O. SB tạo với đáy một góc \(30^o\) . Tính khoảng cách từ O đến mp(SAD)
cho hình chóp tứ giác S.ABCD có ABCD là hình vuông tâm O. SB tạo với đáy một góc 30o . Tính khoảng cách từ O đến mp(SAD)
Lời giải:
Kẻ $OT\perp AD$ và $OH\perp ST$
Vì $S.ABCD$ là chóp tứ giác đều nên $SO\perp (ABCD)$. Do đó:
$\angle (SB, (ABCD))=\angle (SB, BO)=\angle SBO=30^0$
$\frac{SO}{BO}=\tan \angle SBO=\tan 30^0$
$\Rightarrow SO=BO.\tan 30^0=\frac{a\sqrt{2}}{2}.\frac{\sqrt{3}}{3}=\frac{a\sqrt{6}}{6}$
Lại có:
$OT\perp AD, SO\perp AD\Rightarrow (SOT)\perp AD$
$\Rightarrow OH\perp AD$
Mà $OH\perp ST$
$\Rightarrow OH\perp (SAD)$
Nên $OH=d(O, (SAD))$. Theo hệ thức lượng giác vuông:
$\frac{1}{OH^2}=\frac{1}{SO^2}+\frac{1}{OT^2}=\frac{6}{a^2}+\frac{4}{a^2}$
$\Rightarrow OH=\frac{a\sqrt{10}}{10}$
Đúng 2
Bình luận (0)
Bạn coi lại đề xem có thiếu dữ kiện gì không?
Đúng 0
Bình luận (1)
cho hình chóp tứ giác S.ABCD biết đáy ABCD là hình vuông tâm O,cạnh a,SD vuông góc (ABCD).a)chứng minh AC vuông góc (SBD),b)chứng minh (SAD)vuông góc (SAB).c)Tính khoảng cách từ điểm A đến mp(SBD)
a: AC vuông góc BD
AC vuông góc SD
=>AC vuông góc (SBD)
b: AD vuông góc AB
AB vuông góc SD
=>AB vuông góc (ADS)
=>(SAD) vuông góc (SAB)
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O. Khoảng cách từ điểm O đến mặt phẳng (SCD) bằng
a
14
7
và góc giữa đường thẳng SB với mặt đáy bằng 60°. Tính thể tích V của khối chóp S.ABC theo a. A.
V
3
a
3
2
2...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O. Khoảng cách từ điểm O đến mặt phẳng (SCD) bằng a 14 7 và góc giữa đường thẳng SB với mặt đáy bằng 60°. Tính thể tích V của khối chóp S.ABC theo a.
A. V = 3 a 3 2 2
B. V = 3 a 3 2 4
C. V = 3 a 3 2 16
D. V = 9 a 3 2 4
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O; mặt phẳng
S
A
C
vuông góc với mặt phẳng
S
B
D
. Biết khoảng cách từ O đến mặt phẳng
S
A
B
,
S
B
C
,
...
Đọc tiếp
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O; mặt phẳng S A C vuông góc với mặt phẳng S B D . Biết khoảng cách từ O đến mặt phẳng S A B , S B C , S C D lần lượt là 1;2; 5 . Tính khảng cách d từ O đến mặt phẳng S A D
A. d = 20 19
B. d = 19 20
C. d = 2
D. d = 2 2
Chọn đáp án A
Cách 1:
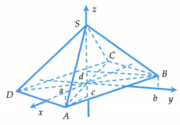
Lấy mặt phẳng α vuông góc với SO cắt (SAC), (SBD) theo các giao tuyến x’Ox, y’Oy.
![]()
Chọn hệ tọa độ Oxyz sao cho tia Oz trùng với tia OS
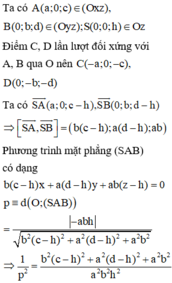
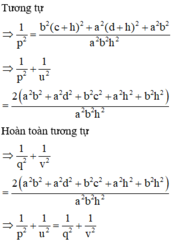

Cách 2:
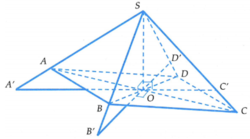
Trong mặt phẳng (SAC) dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng SA, SC lần lượt tại A’, C’
Trong mặt phẳng (SBD) dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng SB, SD lần lượt tại B’, D’
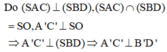
Khi đó tứ diện OSA’B’ có OS, OA’, OB’ đôi một vuông góc nên ta chứng minh được
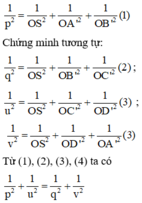
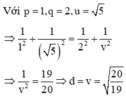
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD đáy là hình vuông cạnh a , tâm O. SA vuông góc với đáy và S4=a căn 6. 1) Chứng minh SB L BC 2) Tính góc giữa SD và mp(ABCD) 3) Tính góc giữa mp(SBC) và mp(ABCD) 4) Tỉnh khoảng cách từ O đến mp(SCD) 5) Tính khoảng cách giữa hai đường thẳng SB và AC
1: AC=căn a^2+a^2=a*căn 2
=>SC=căn SA^2+AC^2=a*căn 8
SB=căn AB^2+SA^2=a*căn 7
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
=>SB vuông góc BC
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a.Cạnh bên SA=acăn15/2 và vuông góc với mặt đáy (ABCD).Tính khoảng cách d từ O đến mp (SBC)
\(\left\{{}\begin{matrix}AO\cap\left(SBC\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SBC\right)\right)=2d\left(O;\left(SBC\right)\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Từ A kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{285}}{19}\)
\(\Rightarrow d\left(O;\left(SBC\right)\right)=\dfrac{1}{2}AH=\dfrac{a\sqrt{285}}{38}\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh có độ dài là a, tâm của hình vuông là O. Có SA vuông góc với đáy và gócgiữa đường thẳng SD và mp(ABCD) bằng030.Gọi I, J lần lượt là trung điểm của cạnh SB và SD.a). Tính khoảng cách từ điểm S đến mp(ABCD).b). Chứng minh các mặt bên của hình chóp là các tam giác vuông.c). Chứng minh: (SBD)(SAC)⊥.d). Chứng minh: IJ(SAC)⊥.e). Tính góc giữa đường thẳng SC và mp(ABCD).f). Tính góc giữa đường thẳng SC và mp(SAB).g). Tính góc giữa đường thẳng SC và mp...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh có độ dài là a, tâm của hình vuông là O. Có SA vuông góc với đáy và gócgiữa đường thẳng SD và mp(ABCD) bằng030.Gọi I, J lần lượt là trung điểm của cạnh SB và SD.
a). Tính khoảng cách từ điểm S đến mp(ABCD).
b). Chứng minh các mặt bên của hình chóp là các tam giác vuông.
c). Chứng minh: (SBD)(SAC)⊥.d). Chứng minh: IJ(SAC)⊥.
e). Tính góc giữa đường thẳng SC và mp(ABCD).
f). Tính góc giữa đường thẳng SC và mp(SAB).
g). Tính góc giữa đường thẳng SC và mp(SAD).
h). Tính góc hợp bởi hai mặt phẳng (SBD) và (ABCD).
i). Tính góc hợp bởi hai mặt phẳng (SBC) và (ABCD).
j). Tính khoảngcách từ điểm A đến mp(SBC).
k). Tính khoảng cách từ điểm A đến mp(SCD).
l). Tính khoảng cách từ điểm A đến mp(SBD).
m). Tính khoảng cách giữa hai đường thẳng chéo nhau BD và SC













