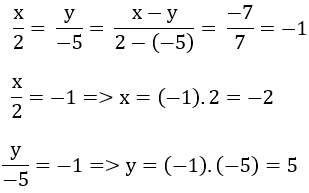Tìm x,y biết:x/5=y/4 và x^2-y^2=1

Những câu hỏi liên quan
\(Tìm x biết:x/5=y/4 và x^2-y^2=4(x,y>0)\)
Vì x, y > 0
Đặt \(\frac{x}{5}=\frac{y}{4}=k\Rightarrow\hept{\begin{cases}x=5k\\y=4k\end{cases}}\)( k > 0 )
x2 - y2 = 4
<=> ( 5k )2 - ( 4k )2 = 4
<=> 25k2 - 16k2 = 4
<=> 9k2 = 4
<=> k2 = 4/9
<=> k = 2/3 ( vì k > 0 )
=> \(\hept{\begin{cases}x=5\cdot\frac{2}{3}=\frac{10}{3}\\y=4\cdot\frac{2}{3}=\frac{8}{3}\end{cases}}\)
heeweghjk/k uubunnnnnnnnnnbhtytcvbyu74xui b bbbbfk44xxxxxxxxxxxxxxxxxxxx56yh6 6rrrrr6r iiiii6irixmx rj 6 5556666666crlxxx8 rr6xxxxxxxxxxxxxxtr4444 tyjrttttttttttttttttr5xyyu
Ta có x/5=y/5=k
=>x=5k;y=4k
Theo tính chất dãy tỉ số = nhau ta có
x/5=y/4=x^2-y^2/5^2-4^2=4/9
x/5=4/9=>x=4/9.5=20/9
y/4=4/9=>y=4/9.4=16/9
=>x=20/9;y=16/9
Xem thêm câu trả lời
a)tìm x,y biết:x-1/y+2 và x+y=23
b)tìm x biết: 4^5+4^5+4^5+4^5/3^5+3^5+3^5.6^5+6^5+6^5+6^5+6^5+6^5/2^5+2^5=8^2x-6
Theo đề ra, ta có: \(\frac{x-1}{y+2}=\frac{3}{5}\)
\(\Rightarrow\frac{x-1}{3}=\frac{y+2}{5}=\frac{x-1+y+2}{8}=\frac{23-1+2}{8}=\frac{24}{8}=3\)
\(\frac{x-1}{3}=3\Rightarrow x=3.3+1=10\)
\(\frac{y+2}{5}=3\Rightarrow y=5.3-2=13\)
Tìm 2 số x và y,biết:x:2=y:(-5) và x-y=-7
tìm x,y biết:
x/-5=y/4=2
x/3=2/y;x,y ∈ Z
a, Xét \(\dfrac{x}{-5}=2\Rightarrow x=-10\)
\(\dfrac{y}{4}=2\Leftrightarrow y=8\)
b, \(xy=6\Rightarrow x;y\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| x | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| y | 6 | -6 | 3 | -3 | 2 | -2 | 1 | -1 |
Đúng 2
Bình luận (1)
tìm hai số x,y biết:x/5 =y/3 và x-y=-2
Ta có : `x/5=y/3` và `x-y=-2`
ADTC dãy tỉ số bằng nhau ta có :
`x/5 = y/3 =(x-y)/(5-3)=(-2)/2=-1`
`=>x/5=-1=>x=-1.5=-5`
`=>y/3=-1=>y=-1.3=-3`
Vậy `x=-5;y=-3`
Đúng 3
Bình luận (0)
Áp dụng tính chất của DTSBN, ta được:
x/5=y/3=(x-y)/(5-3)=-2/2=-1
=>x=-5; y=-3
Đúng 0
Bình luận (0)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{x-y}{5-3}=\dfrac{-2}{2}=-1\)
Suy ra \(\dfrac{x}{5}=-1=>x=-1.5=>x=-5\)
\(\dfrac{y}{3}=-1=>y=-1.3=-3\)
Vậy x=-5; y=-3
Đúng 1
Bình luận (0)
Tìm x;y;z biết:
x/2=y/3=z/5 và x + y - z = 10
2 + 3 - 5 = 0 (ở dưới mẫu) thì vô lí nên đề sai ![]()
Đúng 0
Bình luận (0)
Sửa đề: x+y+z=10
Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}\)
mà x+y+z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y+z}{2+3+5}=\dfrac{10}{10}=1\)
Do đó: x=2; y=3; z=5
Đúng 0
Bình luận (0)
Tìm các số dương x và y biết:x2+y2+1/x2+1/y2=4. Tks các bạn
\(x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=4\)
\(\Leftrightarrow x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}-4=0\)
\(\Leftrightarrow\left(x^2-2.x.\frac{1}{x}+\frac{1}{x^2}\right)+\left(y^2-2.y.\frac{1}{y}+\frac{1}{y^2}\right)=0\)
\(\Leftrightarrow\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2=0\)(1)
Ta thấy \(\left(x-\frac{1}{x}\right)^2\ge0;\left(y-\frac{1}{y}\right)^2\ge0\forall x;y\) nên \(\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2\ge0\forall x;y\)
Để (1) xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x-\frac{1}{x}\right)^2=0\\\left(y-\frac{1}{y}\right)^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{x}\\y=\frac{1}{y}\end{cases}\Rightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}}\)
Vậy \(x=y=1\)
Đúng 0
Bình luận (0)
Tìm x, y biết:
x/y = 2/5 ; x . y = 40
\(\dfrac{x}{y}=\dfrac{2}{5}=\dfrac{x}{2}=\dfrac{y}{5}\)
Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=k2\\y=k5\end{matrix}\right.\)
mà \(xy=40\)
\(\Rightarrow2k.5k=40\)
\(\Rightarrow k^2=4\)
\(\Rightarrow k=\pm4\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{5}=4\\\dfrac{x}{2}=\dfrac{y}{5}=-4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=8;y=20\\x=-8;y=-20\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm x,y,z biết:x/y=2/3; y/z=3/4 và x+y+z=27