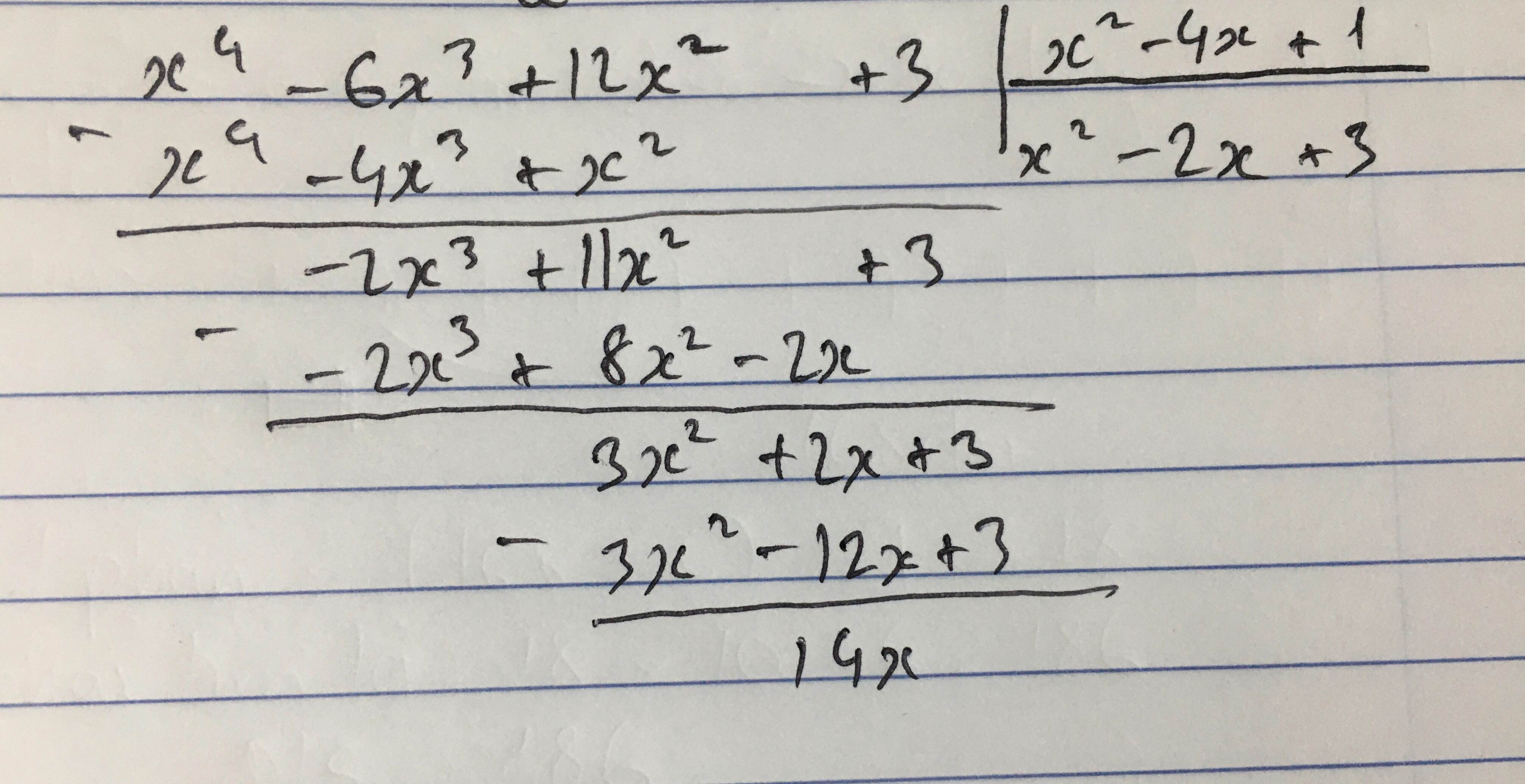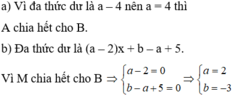Tim a để đa thức x4+6x3+7x2-6x+a chia hết cho x2+3x-1

Những câu hỏi liên quan
Tìm nÎZ để giá trị của biểu thức n3 -2n2 + 3n + 3 chia hết cho giá trị của biểu thức n-1
b) Tìm a để đa thức x4 + 6x3 + 7x2 - 6x + a chia hết cho đa thức x2 + 3x - 1
\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)
Đúng 1
Bình luận (0)
\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)
Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)
\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử:a)
x
4
-
6
x
3
+
12
x
2
- 14x + 3.b)
x
4
+
6
x
3
+
7
x
2
-6x +...
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) x 4 - 6 x 3 + 12 x 2 - 14x + 3.
b) x 4 + 6 x 3 + 7 x 2 -6x + l.
a) ( x 2 – 4x + 1)( x 2 – 2x + 3).
b) ( x 2 + 5x – 1)( x 2 + x – 1).
Đúng 0
Bình luận (0)
a) ( 6x3 - 7x2 - x + 2 ) : ( 2x + 1 )
b) ( x4 - x3 + x2 + 3x ) : ( x2 - 2x + 3 )
\(a,=\left(6x^3+3x^2-10x^2-5x+4x+2\right):\left(2x+1\right)\\ =\left(2x+1\right)\left(3x^2-5x+2\right):\left(2x+1\right)=3x^2-5x+2\\ b,=\left(x^4-2x^3+3x^2+x^3-2x^2+3x\right):\left(x^2-2x+3\right)\\ =\left(x^2-2x+3\right)\left(x^2+x\right):\left(x^2-2x+3\right)=x^2+x\)
Đúng 1
Bình luận (0)
Tìm a để đa thức A chia hết cho đa thức B với:
A = 2 x 3 - 7 x 2 - 11x + a - 8 và B = 2 x 2 + 3x + 4.
Thực hiện chia đa thức A cho B được đa hức dư là a + 12
Từ A chia hết cho B Þ a + 12 = 0 Û a = -12.
Đúng 0
Bình luận (0)
Cho đa thức: A=x4-7x3+10x2+(a-1)x+b-a và B=x2-6x+5. Tìm a và b để đa thức A chia hết cho đa thức B
Ta thấy \(B=\left(x-1\right)\left(x-5\right)\) nên để đa thức A chia hết cho đa thức B thì \(A=\left(x-1\right)\left(x-5\right).C\) với \(C\) là một đa thức bậc 2 hệ số nguyên theo \(x\).
Điều này tương đương với việc \(A\) có 2 nghiệm là \(x=1,x=5\). Do đó \(A\left(1\right)=0\) \(\Leftrightarrow1^4-7.1^3+10.1^2+\left(a-1\right)+b-a=0\) \(\Leftrightarrow b=-3\)
Ta viết lại \(A=x^4-7x^3+10x^2+\left(a-1\right)x-3-a\). Ta có \(A\left(5\right)=0\) \(\Leftrightarrow5^4-7.5^3+10.5^2+\left(a-1\right).5-3-a=0\) \(\Leftrightarrow4a-8=0\) \(\Leftrightarrow a=2\).
Vậy để đa thức A chia hết cho đa thức B thì \(a=2,b=-3\).
Đúng 3
Bình luận (0)
A:B=x2-x+11 dư (a+70)x+b-a-55
Để A chia hết cho B thì
(a+70)x+b-a-55=0
b-a-55=0 (a khác -70) tại x=0
Vậy b-a=55 thỏa đề bài
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử : x4 + 6x3 + 7x2 – 6x + 1
\(x^4+6x^3+7x^2-6x+1\)
\(=x^4-2x^2+1+6x^3+9x^2-6x\)
\(=\left(x^2-1\right)^2+6x\left(x^2-1\right)+9x^2\)
\(=\left(x^2+3x-1\right)^2\)
Đúng 0
Bình luận (0)
Các bạn ơi giúp mik với mik đang cần gấp ạ. Cảm ơn
Cho đa thức: P(x)=6x3−7x2−16x+mP(x)=6x3−7x2−16x+m
a) Tìm m để P(x) chia hết cho 2x+3.
b) Với m vừa tìm được ở câu a, hãy tìm số dư R khi chia P(x) cho 3x-2.
c) Với m vừa tìm đc. Hãy phân tích P(x) thành nhân tử.
Chia đa thức cho đa thức:
(12x2+3-6x3+x4) : (1-4x+x2)
\(\dfrac{x^4-6x^3+12x^2+3}{x^2-4x+1}\)
\(=\dfrac{x^4-4x^3+x^2-2x^3+8x^2-2x+2x^2-8x+2+10x+1}{x^2-4x+1}\)
\(=x^2-2x+2+\dfrac{10x+1}{x^2-4x+1}\)
Đúng 0
Bình luận (0)
Tìm a và b để đa thức A chia hết cho đa thức B với:a) A
x
3
-
9
x
2
+17x - 25 + a và B
x
2
- 2x + 3;b) A
x
4
-
7
x
3
+
10
x
2
+(a - 1)x + b...
Đọc tiếp
Tìm a và b để đa thức A chia hết cho đa thức B với:
a) A = x 3 - 9 x 2 +17x - 25 + a và B = x 2 - 2x + 3;
b) A = x 4 - 7 x 3 + 10 x 2 +(a - 1)x + b - a và B = x 2 -6x + 5.
Tìm a, b để đa thức
A
(
x
)
2
x
3
+
7
x
2
+
a
x
+
b
chia hết cho đa thức
B
(
x
)
x
2
+
x
...
Đọc tiếp
Tìm a, b để đa thức A ( x ) = 2 x 3 + 7 x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 + x – 1
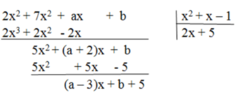
A(x) chia hết cho B(x) khi (a – 3)x + b + 5 là đa thức 0
⇒ a – 3 = 0 hoặc b + 5 = 0 ⇒ a = 3 hoặc b = -5
Đúng 0
Bình luận (0)