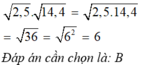\(a,\sqrt{45.8}=\sqrt{360}=\sqrt{6^2.10}=6\sqrt{10}\)

\(b,\sqrt{2,5.14,4}=\sqrt{36}=\sqrt{6^2}=6\)

\(c,\sqrt{10.40}=\sqrt{400}=\sqrt{20^2}=20\)

\(d,\sqrt{52}.\sqrt{13}=\sqrt{52.13}=\sqrt{676}=\sqrt{26^2}=26\)

\(\sqrt{2,5.14,4}=\sqrt{36}=+-6\)

a)\(\sqrt{45.80}=\sqrt{9.400}=\sqrt{9}.\sqrt{400}=3.20=60\)

b) \(\sqrt{75.48}=\sqrt{25.3.16.3}=\sqrt{5^2.3^2.4^2}=5.4.3=60\)

c)\(\sqrt{90.6,4}=\sqrt{10.9.4.1,6}=\sqrt{4^2.3^2.2^2}=4.3.2=24\)

d) \(\sqrt{2,5.14,4}=\sqrt{\dfrac{25}{10}.\dfrac{144}{10}}=\sqrt{\dfrac{25.144}{100}}=\sqrt{\left(\dfrac{5.12}{10}\right)^2}=\dfrac{5.12}{10}=6\)

a) \(\sqrt{45.80}=\sqrt{9.400}=\sqrt{9}.\sqrt{400}=3.20=60\)

b)\(\sqrt{75.48}=\sqrt{25.3.3.16}=5.3.4=60\)

c)\(\sqrt{90.6,4}=\sqrt{9.64}=3.8=24\)

d)\(\sqrt{2,5.14,4}=\sqrt{\dfrac{25}{10}.\dfrac{144}{10}}=\sqrt{\dfrac{25.144}{100}=\dfrac{5.12}{10}=\dfrac{60}{10}=6}\)

a)\(\sqrt{75\cdot48}=\sqrt{25\cdot3\cdot48}=\sqrt{25\cdot144}=\sqrt{25}\cdot\sqrt{144}=5\cdot12=60\)

b) \(\sqrt{2,5\cdot14,4}=\sqrt{25\cdot144\cdot\frac{1}{100}}=\sqrt{25}\cdot\sqrt{144}\cdot\sqrt{\frac{1}{100}}=5\cdot12\cdot\frac{1}{10}=6\)

\(\sqrt{2,5.14,4}=\sqrt{2,5.10.1,44}=\sqrt{25.1,44}=\sqrt{25}.\sqrt{1,44}\)

\(=5.1,2=6\)

2 , 5 . 14 , 4 = 25 . 1 , 44 = 25 . 1 , 44 = 5 . 1 , 2 = 6

cosi đi 

trong quyển nâng cao phát triển toán 9 đó

rất bổ ích đấy mua về mà đọc 

tham khảo nhé bạn :)

https://olm.vn/hoi-dap/detail/222829035519.html