Những câu hỏi liên quan
Cho tam giác ABC nhọn có các đường cao AD, BE, CF cắt nhau tại H.
Chứng minh rằng: AE.BF.CD = AF.BD.CE = DE.EF.FD.
Giúp mình với :<
cho tam giác nhọn ABC có đường cao AD, BE, CF. chứng minh AF.BD.CE = AB.BC.AC. cosA. cosB. cosC.
Cho tam giác ABC có ba góc nhọn với các đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng:
a) Sabc = 1/2.AB.BC.sinB và AE.BF.CD = AB.BC.CA.cosA.cosB.cosC
b) tanB.tanC = AD/HD
c) H là giao điểm ba đường phân giác trong của tam giác DEF
d) HB.HC/AB.AC + HC.HA/BC.BA + HA.HB/CA.CB = 1
Mn ghi đầy đủ GT, KL với vẽ hình hộ mình nha
Cho tam giác ABC có ba góc nhọn với các đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng:
a) Sabc = 1/2.AB.BC.sinB và AE.BF.CD = AB.BC.CA.cosA.cosB.cosC
b) tanB.tanC = AD/HD
c) H là giao điểm ba đường phân giác trong của tam giác DEF
d) HB.HC/AB.AC + HC.HA/BC.BA + HA.HB/CA.CB = 1
1.Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Gọi I và K lần lượt là hình chiếu của điểm D trên các đường thẳng BE và CF. Chứng minh rằng
1.Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Gọi I và K lần lượt là hình chiếu của điểm D trên các đường thẳng BE và CF. Chứng minh rằng
b.IK //EF
c. Trong các tam giác AEF, BDF, CDE có ít nhất một tam giác có diện tích nhỏ hơn hoặc bằng 1/4 diện tích tam giác ABC
b.IK //EF
Đọc tiếp
1.Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Gọi I và K lần lượt là hình chiếu của điểm D trên các đường thẳng BE và CF. Chứng minh rằng 1.Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Gọi I và K lần lượt là hình chiếu của điểm D trên các đường thẳng BE và CF. Chứng minh rằng b.IK //EF c. Trong các tam giác AEF, BDF, CDE có ít nhất một tam giác có diện tích nhỏ hơn hoặc bằng 1/4 diện tích tam giác ABC b.IK //EF
b: góc HID+góc HKD=180 độ
=>HIDK nội tiếp
=>góc HIK=góc HDK
=>góc HIK=góc HCB
=>góc HIK=góc HEF
=>EF//IK
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Tham khảo:
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau
Đúng 0
Bình luận (0)
) Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau tại H. 1) Chứng minh rằng: AE.AC AF.AB2) Chứng minh rằng tam giác AFE đồng dạng tam giác ACB3) Chứng minh rằng tam giác FHE đồng dạng tam giác BHC4) Chứng minh rằngBF.BA+CE.CA BC2
Đọc tiếp
) Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau tại H.
1) Chứng minh rằng: AE.AC = AF.AB
2) Chứng minh rằng tam giác AFE đồng dạng tam giác ACB
3) Chứng minh rằng tam giác FHE đồng dạng tam giác BHC
4) Chứng minh rằngBF.BA+CE.CA = BC2
1: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF và AE/AB=AF/AC
2: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
=>ΔAEF đồng dạng vơi ΔABC
3: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF/HB=HE/HC
Xét ΔHFE và ΔHBC có
HF/HB=HE/HC
góc FHE=góc BHC
=>ΔFHE đồng dạng với ΔBHC
Đúng 1
Bình luận (0)
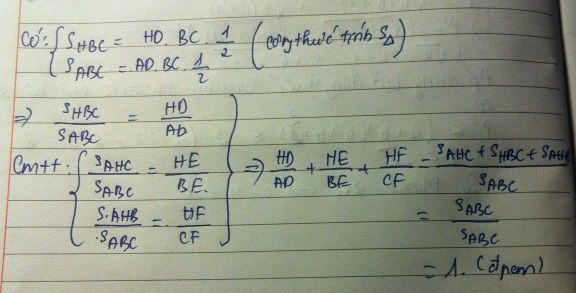
cho tam giác ABC nhọn các đường cao AD, BE, CF cắt nhau tại H chứng minh rằng \(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=1\)
Cho tam giác ABC nhọn. Các đường cao AD,BE, CF cắt nhau tại H. Chứng minh rằng :
a) BD.DC = DH.HA
b) H là giao điểm 3 đường phân giác của tam giác DEF.
c) HD/AD + HE/BE + HF/CF = 1