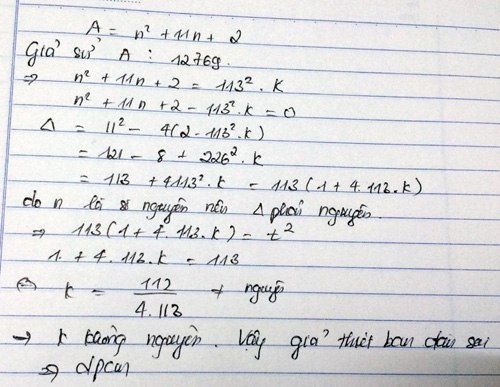chứng minh với mọi số nguyên n thì n^2+11n+39 không chia hết cho `39

Những câu hỏi liên quan
chứng minh rằng với mọi số nguyên n
a) n2+11n+39 không chia hết cho 49
b) n2+n+1 không chia hết cho 9
a) Em tham khảo tại đây nhé:
Câu hỏi của VRCT_Ran love shinichi - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Chứng minh rằng \(n^2+11n+39\) không chia hết cho 49 với mọi số tự nhiên n .
chứng minh nó không chia hết cho 49 là được. dễ mà
Đúng 0
Bình luận (0)
Đặt A=n2+11n+39
Giả sử n2+11n+39 chia hết cho 49 thì A chia hết cho 49 => A cũng chia hết cho 7
Ta có A=n2+11n+39=n2+9n+2n+18+21 = n(n+9)+2(n+9)+21 =(n+9)(n+2)+21
Nhận thấy( n+9)-(n+2)=7
=>Đồng thời (n+9) và (n+2) chia hết cho 7 => (n+9)(n+2) chia hết cho 49
Ta cũng có A chia hết cho 49 mà 21 ko chia hết cho 49 ( vô lí )
Vậy n2+11n+39 ko chia hết cho 49
Đúng 0
Bình luận (0)
Gỉa sử n2 + 11n + 39 \(⋮49\)
\(\Rightarrow\)n2 + 11n + 39 \(⋮7\)
\(\Rightarrow\)n2 + 11n + 39 - 7n - 35 \(⋮7\)
\(\Rightarrow\)n2 + 4n + 4 \(⋮7\)
\(\Rightarrow\)(n + 2)2 \(⋮7\)
\(\Rightarrow\)n + 2 \(⋮7\)
Đặt n + 2 = 7t
\(\Rightarrow\)n2 + 11n + 39 = (7t - 2)2 + 11(7t - 2) + 39
\(\Leftrightarrow\)n2 + 11n + 39 = 49t2 + 49t + 21 ko chia hết cho 49
Điều này mâu thuẫn với điều ta giả sử.
Vậy n2 + 11n + 39 ko chia hết cho 49
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng với mọi n thuộc Z :
a) n^3 -n+4 không chia hết cho 3
b) n^2 +11n +39 không chia hết cho 49
c) A(n) = n( n^2+1)(n^2+4) chia hết cho 5
chứng minh rằng nếu n thuộc Z thì n^2 + 11n +39 không chia hết cho 49
giả sử: A= n^2 + 11n + 39 chia hết cho 49 => A chia hết cho 7
mà : n^2 + 11n + 39 = (n+9)(n+2) +21 chia hết cho 7
=> (n+9)(n+2) chia hết cho 7
lại có: (n+9) - (n+2) = 7 nên (n+9) và (n+2) đồng thời chia hết cho 7
=>(n+9)(n+2) chia hết cho 49
mà: (n+9)(n+2) +21 chia hết cho 49
=> 21 chia hết cho 49 vô lí => đpcm
Bài 2: A=3^ (2*n) + 3^n + 1
n không chia hết cho 3 nên ta xét 2 trường hợp:
* n =3k +1:
A = 3^ (6k + 3) + 3^(3k +1) +1= 9.27^2k +3.27^ +1
= 9.(26+1)^2k + 3.(26 +1)^k +1
= 9(2.13 +1)^2k + 3.(2.13 +1)^k +1
A đồng dư với (9 +3 +1)= 13 theo đồng dư 0 theo (mod 13)
vậy A chia hết cho 13.
( Mình giải thích thêm nhé:
(2.13 +1)^2k chia cho 13 dư 1
=> 9(2.13 +1)^2k chia cho 13 dư 9
(2.13 +1)^k chia 13 dư 1
=> 3.(2.13 +1)^k chia 13 dư 1
=> A chia 13 dư 9 + 3 +1 = 13
A = 13.k +13 với k nguyên
A/13 = k + 1 la số nguyên => A chia hết cho 13
khi triển khai (x+1)^n = thì các hạng tử đều chứa x trừ hạng tử cuối = 1 nên (x+1)^n chia cho x dư 1.)
* n = 3k +2:
A = 3^(6k +4) + 3^(6k +2) +1=81.27^2k +9.27^k +1
= 81.(2.13+1)^2k + 9(2.13 +1)^k +1
A đồng dư với ( 81 + 9 +1) = 91 đồng dư 0 theo (mod 13)
vậy A chia hết cho 13
Đúng 0
Bình luận (0)
Chứng minh bằng phản chứng đơn giản hơn nè
Giả sử có số nguyên n mà n^2 + 11n +39 chia hết cho 49 thì n^2 +11n +39 chia hết cho 7 suy ra n^2 +4n+4 hay (n+2)^2 chia hết cho 7. Suy ra n+2 chia hết cho 7
Vậy n=7k-2
Nhưng khi đó n^2+11n+39 =(7k-2)^2 +11(7k-2) +39 =49k^2 +49k+21 Ko chia hết cho 49( mâu thuẫn rồi nè)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1:Chứng minh rằng n^2+11n +2 không chia hết cho 12769 với mọi số nguyên n.
đúng theo yeu cau tôi giải cho bạn
gia su A=n^2+11n+2 chia het cho 12769
=> n^2+11n+2=113^2.k
<=>n^2+11n+2-113^2.k=0
=>delta(n,k)=113+4.113^2.k=113.(1+4.113k)=t^2
=>1+4.113k=113p^2=>p^2=4k+1/113=>p khong nguyen=> gs ban dau sai=> dpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng n2 + 11n + 2 không chia hết cho 12769 với mọi số nguyên n
Chứng minh rằng n2 + 11n + 2 không chia hết cho 12769 với mọi số nguyên n.
CM bằng cách thế số vào n
Thay n=169,ta đc
1692+11.169+2=30422
Ta thấy : 30422 ko chia hết cho 12769
\(\Rightarrow\)\(n^2+11n+2\)ko chia hết cho 12769 với mọi n
Đúng 0
Bình luận (0)
Chứng minh rằng :Với Vn\(\in N\) thì n2+11n+39 không chia hết cho 39.
Em tham khảo tại đây nhé:
Câu hỏi của VRCT_Ran love shinichi - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số nguyên n thì \(n^2+11n+39\) không chia hết cho 49.
Giả sử \(n^2+11n+39⋮49\) \(\Rightarrow4n^2+44n+156⋮49\)
\(\Rightarrow4n^2+44n+156⋮7\) \(\Leftrightarrow4n^2+2.2n.11+121+35⋮7\)
\(\Leftrightarrow\left(2n+11\right)^2+35⋮7\) mà \(35⋮7\) nên \(\left(2n+11\right)^2⋮7\) mà 7 là số nguyên tố
\(\Rightarrow\left(2n+11\right)^2⋮49\) \(\Rightarrow4n^2+4n+121⋮49\) mà
\(4n^2+4n+121+35⋮49\) nên \(35⋮49\) => vô lý vậy điều giả sử là sai
vậy n^2+11n+39 không chia hết cho 49
Đúng 0
Bình luận (0)