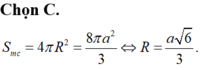Một mặt cầu có diện tích 1256 cm3 . Tính bán kính mặt cầu đó.

Những câu hỏi liên quan
Một hình cầu có số đo diện tích mặt cầu (tính bằng c m 2 ) đúng bằng số đo thể tích của nó (tính bằng c m 3 ). Tính bán kính của hình cầu đó
giúp mik vs mn ơi
Một quả bóng hình cầu có diện tích bề mặt là 1256 cm2 tính bán kính của quả bóng đó (π≈3,14)
Từ công thức \(S_{cầu}=4\pi r^2=1256\left(cm^2\right)\)
\(\Rightarrow r^2=\dfrac{1256}{4\pi}\approx100\left(cm\right)\Rightarrow r\approx10\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06
c
m
2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8
c
m
3
Đọc tiếp
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:
a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 c m 2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8 c m 3
a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3
Đúng 0
Bình luận (0)
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu. A.
R
3
V
S
B.
R
S
3
V
C.
R
4
V
S
D.
R
V
3
S
Đọc tiếp
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
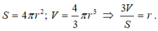
Đúng 0
Bình luận (0)
I. Trắc nghiệm ( 6 điểm)Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu. A.
R
3
V
S
B.
R
S
3
V
C.
R
4
V
S
D.
R
V
3...
Đọc tiếp
I. Trắc nghiệm ( 6 điểm)
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
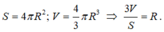
Đúng 0
Bình luận (0)
Cho mặt cầu có diện tích bằng
8
πa
2
3
Tính bán kính mặt cầu đó
A
.
a
3
3
B
.
a
2
3
C
.
a...
Đọc tiếp
Cho mặt cầu có diện tích bằng 8 πa 2 3 Tính bán kính mặt cầu đó
A . a 3 3
B . a 2 3
C . a 6 3
D . 2 a 6 3
Biết rằng khi quay một đường tròn có bán kính bằng 1 quanh đường kính của nó thì ta được một mặt cầu. Tính diện tích mặt cầu đó.
A. 4 π
B. 4 3 π
C. 2 π
D. π
Đáp án A
Ta có: R C = 1 ⇒ S C = 4 πR 2 = 4 π .
Đúng 0
Bình luận (0)
a) Tìm diện tích mặt cầu và thể tích hình cầu, biết bán kính của hình cầu là 4cm
b) Thể tích của một hình cầu là 512π c m 2 . Tính diện tích mặt cầu đó
a, Tính được S = 64π c m 2 và V = 256 π 3 c m 3
b, Tính được S = 211,32π c m 2
Đúng 0
Bình luận (0)
Cho một mặt cầu có diện tích bằng
8
πa
2
3
. Tính bán kính mặt cầu. A.
a
6
3
B.
a
6
5
C.
a
6
7
D. ...
Đọc tiếp
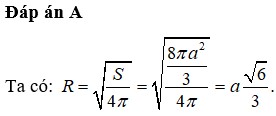
Cho một mặt cầu có diện tích bằng 8 πa 2 3 . Tính bán kính mặt cầu.
A. a 6 3
B. a 6 5
C. a 6 7
D. a 6 15