Đáp án A
Ta có: R C = 1 ⇒ S C = 4 πR 2 = 4 π .
Đáp án A
Ta có: R C = 1 ⇒ S C = 4 πR 2 = 4 π .
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng
A. 3 2
B. 3
C. 1 2
D. 1
Biết rằng khi quay một đường tròn có bán kính bằng 1 quay quanh một đường kính của nó ta được một mặt cầu. Tính diện tích mặt cầu đo
A. 4 3 π
B. 4 π
C. π
D. 2 π
Một hình thang vuông ABCD có đường cao A D = π , đáy nhỏ A B = π , đáy lớn C D = 2 π . Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng:
A. 4 3 π 4
B. 7 3 π 4
C. 10 3 π 4
D. 13 3 π 4
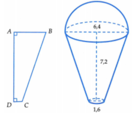
Một cơ sở sản xuất kem chuẩn bị làm 750 chiếc kem giống nhau theo đơn đặt hàng. Cốc đựng kem có dạng hình tròn xoay được tạo thành khi quay hình thang ABCD vuông tại A và D quanh trục AD (xem hình minh họa). Chiếc cốc có bề dày không đáng kể, chiều cao bằng 7,2 cm, đường kính miệng cốc bằng 6,4cm và đường kính đáy cốc bằng 1,6cm. Kem được đổ đầy cốc và dư ra phía ngoài một lượng có dạng nửa hình cầu có bán kính bằng bán kính miệng cốc. Biết rằng 1 d m 3 kem nguyên liệu có giá 62.000 đồng. Hỏi số tiền mà cơ sở đó phải thanh toán tiền kem nguyên liệu để sản xuất 750 chiếc gần với giá trị nào dưới dây nhất? (Lấy π ≈ 3 , 14 ).
A. 7.905.000 đồng.
B. 7.900.500 đồng.
C. 7.899.500 đồng.
D. 7.899.000 đồng.
Diện tích hình tròn lớn của một hình cầu là 2a . Một mặt phẳng (P) cắt hình cầu đó theo đường tròn nhỏ có bán kính r và có diện tích bằng một nửa diện tích đường tròn lớn. Biết bán kính của hình cầu là R, chọn đáp án đúng:
A. R = 2 r 3
B. R = r 2
C. R = 2 2 r
D. R = 2 r
Diện tích hình tròn lớn cùa một hình cầu là 2a. Một mặt phẳng (P) cắt hình cầu đó theo đường tròn nhỏ nhỏ có bán kính r và có diện tích bằng một nửa diện tích đường tròn lớn. Biết bán kính của hình cầu là R, chọn đáp án đúng:a
A. R = 2 r 3
B. R = 2 2 r
C. R = r 2
D. R = 2 r
Cho hình nón có thể tích bằng 12 π và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
A. 4
B. 3.
C. 6
D. 5
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-1;-1),B(4;-5;-5) và mặt phẳng (P):x+y+z-3=0. Mặt cầu (S) thay đổi qua hai điểm A,B và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có tâm H và bán kính bằng 3. Biết rằng H luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.
A. 21 .
B. 2 6 .
C. 6.
D. 3 3 .
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng
A. 3 + 2 3 πR 2 3
B. 3 + 2 3 πR 2 2
C. 3 + 2 2 πR 2 2
D. 3 + 2 2 πR 2 3