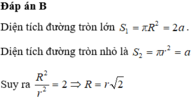Các câu hỏi tương tự
Diện tích hình tròn lớn cùa một hình cầu là 2a. Một mặt phẳng (P) cắt hình cầu đó theo đường tròn nhỏ nhỏ có bán kính r và có diện tích bằng một nửa diện tích đường tròn lớn. Biết bán kính của hình cầu là R, chọn đáp án đúng:a A.
R
2
r
3
B.
R...
Đọc tiếp
Diện tích hình tròn lớn cùa một hình cầu là 2a. Một mặt phẳng (P) cắt hình cầu đó theo đường tròn nhỏ nhỏ có bán kính r và có diện tích bằng một nửa diện tích đường tròn lớn. Biết bán kính của hình cầu là R, chọn đáp án đúng:a
A. R = 2 r 3
B. R = 2 2 r
C. R = r 2
D. R = 2 r
Cho khối cầu tâm O và bán kính R. Xét hai mặt phẳng (P), (Q) thay đổi song song với nhau có khoảng cách là R và cùng cắt khối cầu theo tiết diện là hai hình tròn. Tổng diện tích của hai hình tròn này có giá trị lớn nhất là A.
5
4
πR
2
B.
πR
2
C.
7
4
πR
2
D.
3...
Đọc tiếp
Cho khối cầu tâm O và bán kính R. Xét hai mặt phẳng (P), (Q) thay đổi song song với nhau có khoảng cách là R và cùng cắt khối cầu theo tiết diện là hai hình tròn. Tổng diện tích của hai hình tròn này có giá trị lớn nhất là
A. 5 4 πR 2
B. πR 2
C. 7 4 πR 2
D. 3 2 πR 2
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất. A.
r...
Đọc tiếp
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.
A. r = 3 2 ; h = 6 2
B. r = 6 2 ; h = 3 2
C. r = 6 3 ; h = 3 3
D. r = 3 3 ; h = 6 3
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng A.
3
+
2
3
πR
2
3
B.
3
+
2...
Đọc tiếp
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng
A. 3 + 2 3 πR 2 3
B. 3 + 2 3 πR 2 2
C. 3 + 2 2 πR 2 2
D. 3 + 2 2 πR 2 3
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng A.
3
+
2
3
πR
2
3
B.
3
+
2...
Đọc tiếp
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng
A. 3 + 2 3 πR 2 3
B. 3 + 2 3 πR 2 2
C. 3 + 2 2 πR 2 2
D. 3 + 2 2 πR 2 3
Một khối pha lê gồm một hình cầu (
H
1
) bán kính R và một hình nón (
H
2
) có bán kính đáy và đường sinh lần lượt là r, l thỏa mãn
r
1
3
l
và
l
3
2
R
xếp chồng lên nhau (hình vẽ). Biết tổng diện tích mặt cầu (
H
1
) và diện tích t...
Đọc tiếp
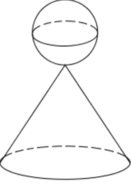
Một khối pha lê gồm một hình cầu ( H 1 ) bán kính R và một hình nón ( H 2 ) có bán kính đáy và đường sinh lần lượt là r, l thỏa mãn r = 1 3 l và l = 3 2 R xếp chồng lên nhau (hình vẽ). Biết tổng diện tích mặt cầu ( H 1 ) và diện tích toàn phần của hình nón ( H 2 ) là 91 c m 2 . Tính diện tích của khối cầu ( H 1 ).
A. 62 c m 2
B. 63 c m 2
C. 64 c m 2
D. 65 c m 2
Cho mặt phẳng (P) cắt mặt cầu S(I;R) theo giao tuyến là đường tròn có bán kính r 3 cmhoảng cách từ I đến (P) bằng 2cm. Diện tích mặt cầu S(I;R) bằng A.
52
π
cm
2
B.
13
π
cm
2
C.
4
13
π
cm
2
D.
4
5
π
c...
Đọc tiếp
Cho mặt phẳng (P) cắt mặt cầu S(I;R) theo giao tuyến là đường tròn có bán kính r = 3 cmhoảng cách từ I đến (P) bằng 2cm. Diện tích mặt cầu S(I;R) bằng
A. 52 π cm 2
B. 13 π cm 2
C. 4 13 π cm 2
D. 4 5 π cm 2
Cho hình cầu (S) tâm I bán kính R. Một mặt phẳng (P) cắt mặt cầu (S) theo đường tròn giao tuyến (L). Khối nón đỉnh I và đáy là đường tròn (L) có thể tích lớn nhất là
a
π
R
3
b
3
(
a
,
b
∈
N
)
. Hỏi a+b bằng? A. 10 B. 9 C. 11 D. 13
Đọc tiếp
Cho hình cầu (S) tâm I bán kính R. Một mặt phẳng (P) cắt mặt cầu (S) theo đường tròn giao tuyến (L). Khối nón đỉnh I và đáy là đường tròn (L) có thể tích lớn nhất là a π R 3 b 3 ( a , b ∈ N ) . Hỏi a+b bằng?
A. 10
B. 9
C. 11
D. 13
Cho một hình trụ có hai đáy là hai hình tròn tâm O và Ocó bán kính R và chiều cao bằng R
2
. Mặt phẳng (P) đi qua OO cắt hình trụ theo một thiết diện có diện tích bằng bao nhiêu? A.
2
2
R
2
. B.
2
R
2
. C. ...
Đọc tiếp
Cho một hình trụ có hai đáy là hai hình tròn tâm O và O'có bán kính R và chiều cao bằng R 2 . Mặt phẳng (P) đi qua OO' cắt hình trụ theo một thiết diện có diện tích bằng bao nhiêu?
A. 2 2 R 2 .
B. 2 R 2 .
C. 2 R 2 .
D. 4 R 2 .