HD: Gọi x, y lần lượt là khoảng cách từ tâm mặt cầu đến các đường tròn thiết diện
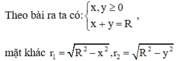
Tổng diện tích của hai hình tròn này là:
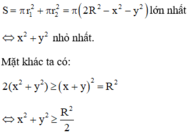
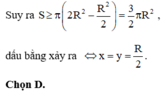
HD: Gọi x, y lần lượt là khoảng cách từ tâm mặt cầu đến các đường tròn thiết diện
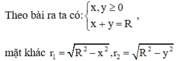
Tổng diện tích của hai hình tròn này là:
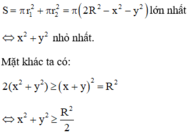
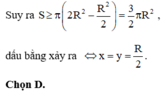
Cho mặt cầu (S) tâm O, bán kính R. Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình trụ (T) nội tiếp mặt cầu (S) có một đáy là đường tròn (C) và có chiều cao là h ( h > 0 ) . Tính h để khối trụ (T) có giá trị lớn nhất
A. h = 2 R 3
B. h = 2 R 3 3
C. h = R 3
D. h = R 3 3
Cho mặt cầu tâm O, bán kính R. Xét mặt phẳng (P) thay đổi và cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón (N) có đỉnh S nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao là h (h>R). Tính h để thể tích khối nón được tạo nên bởi (N) có giả trị lớn nhất.
A. h = R 3
B. h = R 2
C. h = 4 R 3
D. h = 3 R 2
Cho khối cầu tâm (O) bán kính 6cm. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, khi đó giá trị của x là:
A. 2 cm
B. 3 cm
C. 4 cm
D. 0 cm
Cho khối cầu tâm O, bán kính 6cm. Mặt phẳng (P) cách O một khoảng h cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của h bằng
A. 2cm
B. 3cm
C. 4cm
D. 0cm
Cho khối tâm cầu O bán kính bằng 6cm. Mặt phẳng (P) cách O một khoảng là x, cắt khối cầu theo một hình tròn (C). Một khội nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng
A. 2cm
B. 3cm
C. 4cm
D. 0cm
Cho một khối cầu tâm O bán kính bằng 6cm. Mặt phẳng (P) cách O một khoảng x (cm) cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng
A. 2cm
B. 3cm.
C. 4cm
D. 0cm
Cho đường tròn (C) tâm O, bán kính bằng 1, đường tròn (T) tâm I, bán kính bằng 2 lần lượt nằm trên hai mặt phẳng song song với nhau. Biết khoảng cách giữa hai mặt phẳng song song đó bằng độ dài đoạn thẳng OI = 3. Tính diện tích mặt cầu đi qua hai đường tròn (C) và (T)
A. 24p.
B. 20p
C. 16p
D. 12p
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm O 1 ( O 1 nằm giữa O và O') cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích bằng nhau
A. x = R 3 + R ' 3 6 3
B. x = R 3 + R ' 3 4 3
C. x = R 3 + R ' 3 3 3
D. x = R 3 + R ' 3 2 3
Trong không gian Oxyz, cho mặt cầu S 1 có tâm I 2 ; 1 ; 1 bán kính bằng 4 và mặt cầu S 2 có tâm J 2 ; 1 ; 5 bán kính bằng 2. (P) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu S 1 , S 2 . Đặt M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ O đến mặt phẳng Giá trị M + m bằng:
A. 8
B. 8 3 .
C. 9
D. 15 .