Cho DeltaABC vuông tại A, đường cao AH. D và E lần lượt là hình chiếu của H trên AB, AC. Qua D và E kẻ các đường thẳng vuông góc với DE lần lượt cắt BC tại M, N.a, Chứng minh AB.ADAE.ACb, Chứng minh AD.BD+AE.ECAH2c, Chứng minh M, N lần lượt là trung điểm của BH, CHd, Chứng minh frac{CE}{BD}frac{AC^3}{AB^3}e, Chứng minh sqrt[3]{BC^2}sqrt[3]{BD^2}+sqrt[3]{CE^2}Ai biết bài này làm ơn giải giúp mình câu e với, các câu còn lại mình làm được rồi. Cám ơn trước nha!
Đọc tiếp
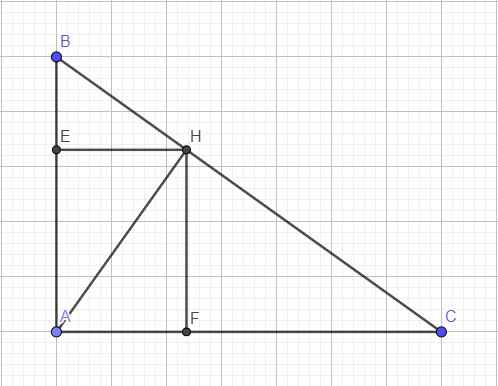
Cho \(\Delta\)ABC vuông tại A, đường cao AH. D và E lần lượt là hình chiếu của H trên AB, AC. Qua D và E kẻ các đường thẳng vuông góc với DE lần lượt cắt BC tại M, N.
a, Chứng minh AB.AD=AE.AC
b, Chứng minh AD.BD+AE.EC=AH2
c, Chứng minh M, N lần lượt là trung điểm của BH, CH
d, Chứng minh \(\frac{CE}{BD}=\frac{AC^3}{AB^3}\)
e, Chứng minh \(\sqrt[3]{BC^2}=\sqrt[3]{BD^2}+\sqrt[3]{CE^2}\)
Ai biết bài này làm ơn giải giúp mình câu e với, các câu còn lại mình làm được rồi. Cám ơn trước nha!