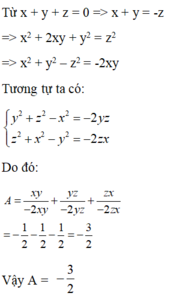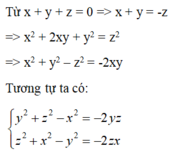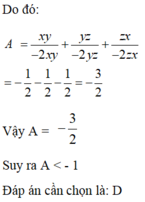Cho ba số x, y và z thỏa mãn x + y + z = 0. Chứng minh rằng
2(x5 + y5 + z5) = 5xyz(x2 + y2 + z2).

Những câu hỏi liên quan
CMR: nếu x+y+z =0 thì :
2(x5+y5+z5)=5xyz(x2+y2+z2).
x + y + z = 0 ⇒ x 3 + y 3 + z 3 = 3 x y z ⇒ ( x 3 + y 3 + z 3 ) ( x 2 + y 2 + z 2 ) = 3 x y z ( x 2 + y 2 + z 2 ) ⇒ x 5 + y 5 + z 5 + x 2 y 2 ( x + y ) + y 2 z 2 ( y + z ) + z 2 x 2 ( z + x ) = 3 x y z ( x 2 + y 2 + z 2 ) ⇒ x 5 + y 5 + z 5 − x y z ( x y + y x + z x ) = 3 x y z ( x 2 + y 2 + z 2 ) ⇒ 2 ( x 5 + y 5 + z 5 ) = 5 x y z ( x 2 + y 2 + z 2)
Đúng 3
Bình luận (1)
cho xyz khác 0 và thỏa mãn x2=y.z,y2=x.z,z2 =x.y. chứng minh x =y=z
\(x^2=y.z\Rightarrow x^3=x.y.z\\ y^2=x.z\Rightarrow y^3=x.y.z\\ z^2=x.y\Rightarrow z^3=x.y.z\\ \Rightarrow x^3=y^3=z^3\\ \Rightarrow x=y=z\)
Đúng 1
Bình luận (0)
chứng minh rằng , với mọi số thực x,y,z ta có
(z+x-y)x5+(x+y-z)y5+(y+z-x)z5≥0
Vẫn đề đó hả em
Câu này dùng BĐT Schur là ra luôn cx đc, nhưng mà thế thì hơi mất hứng, anh thử đề xuất phương án này ha
VT=\(cyc\sum x^5.\left(x-y+z\right)\) Gấp đôi vế trái lên và phá ngoặc ra nhóm về kiểu này
2.VT=(x^6-2x^5y+2xy^5+y^6)+.......tương tự như thế ha
Giờ chỉ cần mỗi cái ngoặc này >=0 là cả lũ >=0 do tương tự
Mà \(x^6-2x^5y+2xy^5+y^6=\left(x^2+y^2\right).\left(x^2-xy-y^2\right)^2\) (Cái này em nhóm 2 cái cuối, 2 cái giữa xong triển khai ra là đc)
Dễ thấy x^2+y^2>=0, cái ngoặc kia là bình phương cũng >=0
Do đó cái TH kia >=0. Các th còn lại thì cx tương tự
Cộng vế với vế suy ra 2VT>=0, Hay VT>=0 (đpcm)
Đúng 1
Bình luận (0)
Anh gửi riêng phần phân tích này
\(x^6-2x^5y+2xy^5+y^6=\left(x^2+y^2\right)\left(x^4-x^2y^2+y^4\right)-2xy\left(x^2+y^2\right)\left(x^2-y^2\right)=\left(x^2+y^2\right).\left(x^4-x^2y^2+y^4-2xy\left(x^2-y^2\right)\right)=\left(x^2+y^2\right)\left(\left(x^4-2x^2y^2+y^4\right)-2xy\left(x^2-y^2\right)+x^2y^2\right)\)Viết tiếp cái ngoặc to thành bình phương là ra cái anh vt chỗ trên đầu nhé
Thử xem có đc ko
Đúng 1
Bình luận (0)
Cho các số thực x, y, z, a, b, c thỏa mãn: x+y+z=1; x2+y2+z2=1 và a/x=b/y=c/z.
Chứng minh rằng: ab + bc + ca =0
Lời giải:
Đặt $\frac{a}{x}=\frac{b}{y}=\frac{c}{z}=t$
$\Rightarrow a=xt; b=yt; c=zt$. Ta có:
$a+b+c=xt+yt+zt=t(x+y+z)=t$
$a^2+b^2+c^2=t^2(x^2+y^2+z^2)=t^2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{t^2-t^2}{2}=0$
Ta có đpcm.
Đúng 1
Bình luận (0)
Cho x; y; z ≠ 0 thỏa mãn x + y + z 0. Tính giá trị biểu thức: A
x
y
x
2
+
y
2
−
z
2
+
y
z
y
2
+...
Đọc tiếp
Cho x; y; z ≠ 0 thỏa mãn x + y + z = 0. Tính giá trị biểu thức: A = x y x 2 + y 2 − z 2 + y z y 2 + z 2 − x 2 + z x z 2 + x 2 − y 2
A. A = 1 2
B. A = - 1 2
C. A = - 3 2
D. A = 3 2
Cho x; y; z ≠ 0 thỏa mãn x + y + z 0. Chọn câu đúng về biểu thức
A
x
y
x
2
+
y
2
−
z
2
+
y
z
y
2...
Đọc tiếp
Cho x; y; z ≠ 0 thỏa mãn x + y + z = 0. Chọn câu đúng về biểu thức A = x y x 2 + y 2 − z 2 + y z y 2 + z 2 − x 2 + z x z 2 + x 2 − y 2
A. A < -2
B.0 < A < 1
C. A > 0
D. A < -1
cho x, y, z ≥ 0 thỏa mãn x + y + z =6. Tìm GTNN và GTLN của
A = x2 + y2 + z2
Bạn tham khảo lời giải tại đây:
cho \(x,y,z\ge0\) thỏa mãn \(x y z=6\). tìm GTLN và GTNN của biểu thức \(A=x^2 y^2 z^2\) - Hoc24
Đúng 0
Bình luận (0)
z√(12+x2)(12+y2)12+z2
Đọc tiếp
Đề lỗi công thức rồi. Bạn xem lại.
Đúng 0
Bình luận (0)
Cho x,y,z là số dương thoa mãn x2+y2-z2>0 Chứng minh x+y-z>0