Chứng minh x4+3x2+3 vô nghiệm

Những câu hỏi liên quan
Chứng minh đa thức x4+2x2+1 vô nghiệm
x4+2x2+1
Ta có :
x4 ≥ 0 ∀ x
x2 ≥ 0 ∀ x => 2x2 ≥ 0 ∀ x
=> x4+2x2+1 ≥ 1 >0
Suy ra đa thức trên vô nghiệm
Đúng 1
Bình luận (0)
chứng minh phương trình sau vô nghiệm:
x4-2x3+10x+30=0
Giải:
Tập xác định của phương trình
x\(\varepsilon\) (\(\infty\);\(\infty\)
Tìm GTLN của -3x^2+6x+10
Chứng minh F(x)=x^6-2x^3+3x^2-5x+1/2x^3+12+3x2-6x vô nghiệm
Đồ thị sau đây là của hàm số y
x
4
-
3
x
2
-
3
. Với giá trị nào của m thì phương trình
x
4
-
3
x
2
-
3
-
m
có 3 nghiệm phân biệt A. m -4 B. m -3 C. 0 D. m -5
Đọc tiếp
Đồ thị sau đây là của hàm số y = x 4 - 3 x 2 - 3 . Với giá trị nào của m thì phương trình x 4 - 3 x 2 - 3 - m có 3 nghiệm phân biệt
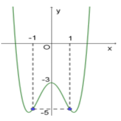
A. m = -4
B. m = -3
C. 0
D. m = -5
Đồ thị sau đây của hàm số y
x
4
-
3
x
2
-
3
. Với giá trị nào của m thì phương trình
x
4
-
3
x
2
+
m
0
có ba nghiệm phân biệt? A. m -4 B. m 0. C. m -3. D. m 4.
Đọc tiếp
Đồ thị sau đây của hàm số y = x 4 - 3 x 2 - 3 . Với giá trị nào của m thì phương trình x 4 - 3 x 2 + m = 0 có ba nghiệm phân biệt?
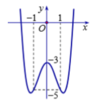
A. m = -4
B. m = 0.
C. m = -3.
D. m = 4.
Chọn B.
Ta có:
x
4
-
3
x
2
+
m
=
0
![]()
Dựa vào đồ thị ta có phương trình có 3 nghiệm phân biệt khi -m-3 = -3 => m = 0
Đúng 0
Bình luận (0)
Đồ thị sau đây của hàm số
y
x
4
-
3
x
2
-
3
.
Với giá trị nào của m thì phương trình
x
4
-
3
x
2...
Đọc tiếp
Đồ thị sau đây của hàm số y = x 4 - 3 x 2 - 3 . Với giá trị nào của m thì phương trình x 4 - 3 x 2 + m = 0 có ba nghiệm phân biệt?
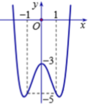
A.m=-4
B.m=0
C.m=-3
D.m=4
Chọn B.
Ta có:
x 4 - 3 x 2 + m = 0 ⇔ x 4 - 3 x 2 = - m ⇔ x 4 - 3 x 2 - 3 = - m - 3 .
Dựa vào đồ thị ta có phương trình có 3 nghiệm phân biệt khi
- m - 3 = - 3 ⇔ m = 0 .
Đúng 0
Bình luận (0)
Đồ thị sau đây là của hàm số
y
x
4
−
3
x
2
−
3.
Với giá trị nào của m thì phương trình
x
4
−
3
x
2
+
m
0
có ba nghiệm phân biệt ? A. m -3 B. m -4 C m 0 D. m 4
Đọc tiếp
Đồ thị sau đây là của hàm số y = x 4 − 3 x 2 − 3. Với giá trị nào của m thì phương trình x 4 − 3 x 2 + m = 0 có ba nghiệm phân biệt ?
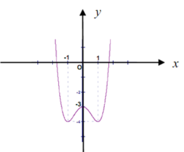
A. m= -3
B. m= -4
C m= 0
D. m= 4
Đáp án C
x 4 − 3 x 2 + m = 0 ( 1 ) ⇔ x 4 − 3 x 2 − 3 = − 3 − m ( * )
Để phương trình (1) có 3 nghiệm phân biệt thì phương trình (*) có 3 nghiệm phân biệt
⇔ − 3 − m = − 3 ⇔ m = 0
Đúng 0
Bình luận (0)
Cho hai đa thức: A(x) = x4 + 2 – 3x2 – x3
và B(x) = 3x2 + x4 + 5
a/ Sắp xếp các hạng tử của đa thức A(x) và B(x) theo lũy thừa giảm dần của biến ?
b/ Tính A(x) + B(x)
c/ Chứng tỏ đa thức B(x) không có nghiệm
a: A(x)=x^4-x^3-3x^2+2
B(x)=x^4+3x^2+5
b: A(x)+B(x)=2x^4-x^3+7
c: B(x)=x^2(x^2+3)+5>0
=>B(x) ko có nghiệm
Đúng 0
Bình luận (0)
Chứng minh rằng
a) – x2 + 4x – 5 < 0 với mọi x
b) x4 + 3x2 + 3 > 0 với mọi x
c) (x2 + 2x + 3)(x2 + 2x + 4) + 3 > 0 với mọi x
a: Ta có: \(-x^2+4x-5\)
\(=-\left(x^2-4x+5\right)\)
\(=-\left(x^2-4x+4+1\right)\)
\(=-\left(x-2\right)^2-1< 0\forall x\)
Đúng 0
Bình luận (1)
b: Ta có: \(x^4\ge0\forall x\)
\(3x^2\ge0\forall x\)
Do đó: \(x^4+3x^2\ge0\forall x\)
\(\Leftrightarrow x^4+3x^2+3>0\forall x\)
c: Ta có: \(\left(x^2+2x+3\right)=\left(x+1\right)^2+2>0\forall x\)
\(x^2+2x+4=\left(x+1\right)^2+3>0\forall x\)
Do đó: \(\left(x^2+2x+3\right)\left(x^2+2x+4\right)>0\forall x\)
\(\Leftrightarrow\left(x^2+2x+3\right)\left(x^2+2x+4\right)+3>0\forall x\)
Đúng 1
Bình luận (0)
Chứng minh rằng
a) – x2 + 4x – 5 < 0 với mọi x
b) x4 + 3x2 + 3 > 0 với mọi x
c) (x2 + 2x + 3)(x2 + 2x + 4) + 3 > 0 với mọi x
b: Ta có: \(x^4\ge0\forall x\)
\(3x^2\ge0\forall x\)
Do đó: \(x^4+3x^2\ge0\forall x\)
\(\Leftrightarrow x^4+3x^2+3>0\forall x\)
c: Ta có: \(\left(x^2+2x+3\right)=\left(x+1\right)^2+2>0\forall x\)
\(x^2+2x+4=\left(x+1\right)^2+3>0\forall x\)
Do đó: \(\left(x^2+2x+3\right)\left(x^2+2x+4\right)>0\forall x\)
\(\Leftrightarrow\left(x^2+2x+3\right)\left(x^2+2x+4\right)+3>0\forall x\)
Đúng 1
Bình luận (0)














