Cho đường tròn (O) và 1 điểm A ngoài đường tròn kẻ các tiếp tuyến AB, AC (B, C là tiếp điểm) với đường tròn gọi H là giao điểm của OA và BC.
A) cm tứ giác ABOC nội tiếp
B) tính độ dài OH
C) tính diện tích tam giác ABC
cho đường tròn tâm o bán kính r và một điểm A nằm ở ngoài đường tròn .qua A kẻ các tiếp tuyến AB và AC với đường tròn (B và C là các tiếp điểm ) .gọi h giao điểm của AO và BC .cm ABOC là tứ giác nội tiếp
góc OBA+góc OCA=90+90=180 độ
=>ABOC nội tiếp
Cho đường tròn tâm O, điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Gọi I là giao điểm của OA và BC.
a) Chứng minh tam giác ABC cân.
b) Chứng minh OA vuông góc với BC.
c) Tính độ dài BI, biết OB = 6 cm; OA = 8 cm. d) Chứng minh rằng : AB 2 – OC 2 = AI 2 – IO2
a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
=>ΔABC cân tại A
b: OB=OC
AB=AC
Do đó: AO là trung trực của BC
=>AO vuông góc với BC
Cho ( O;R) và A ở ngoài đường tròn. qua A kẻ tiếp tuyến AB,AC và đường tròn (B,C là tiếp điểm)
a) Chứng minh: ABOC là tứ giác nội tiếp
b) Gọi H là giao điểm của BC và OA. Chứng minh: BC vuông góc OA
c) Kẻ đường kính BD của đường tròn; kẻ CK vuông góc BD ( K thuộc BD). Chứng minh: CK.CD=AC.KD
d) AD cắt CK ở I. Chứng minh: tam giác OKI đồng dạng tam giác DBA
Cho đường tròn (O) và điểm A nằm ngoài (O). Kẻ các tiếp tuyến AB, AC với (O) trong đó B,C là các tiếp điểm
a, Chứng minh đường thẳng OA là trung trực của BC
b, Gọi H là giao điểm của AO và BC. Biết OB = 2cm và OH = 1 cm, tính:
i, Chu vi và diện tích tam giác ABC
ii, Diện tích tứ giác ABOC
a, HS tự làm
b,i, Áp dụng định lý Pytago tính được BH = 3 cm
Áp dụng hệ thức lược về cạnh góc vuông và đường cao trong tam giác vuông, tính được:
AB = AC = 2 3 cm => P A B C = 6 3 cm, S A B C = 3 3 c m 2
ii, Ta có: S A B O C = S A B C + S B O C = 4 3 c m 2
Cho điểm A nằm ngoài đường tròn (O;R). Vẽ các tiếp tuyến AB, AC với đường tròn (O) tại B và C.
a) CM: tứ giác ABOC nội tiếp được đường tròn
b) Vẽ cát tuyến ADE với đường tròn (O), cát tuyến ADE không qua tâm O; D nằm giữa A và E ). CM: AB^2=AD.AE=OA^2-R^2
c) Gọi H là giao điểm của BC và OA. Cm: tứ giác HDEO nội tiếp
cho đường tròn tâm O A là điểm nằm bên ngoài đường tròn kẻ hai tiếp tuyến AB,AC và cát tuyến AMN của đường tròn tâm O gọi H là giao điểm AO và BC chứng minh
a) tứ giác ABOC nội tiếp đường tròn chỉ rõ tâm và bán kính của đường tròn
b)OA vuông góc BC
c) AM. AN đồng dạng AH.AO .
a: góc ABO+góc ACO=90+90=180 độ
=>ABOC nội tiếp đường tròn đường kính OA
Tâm là trung điểm của OA
Bán kính là OA/2
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>AO vuông góc BC
c: Xét ΔAMB và ΔABN có
góc AMB=góc ABN
góc MAB chung
=>ΔAMB đồng dạng với ΔABN
=>AM/AB=AB/AN
=>AB^2=AM*AN=AH*AO
Từ một điểm A nằm bên ngoài đường tròn (o), kẻ các tiếp tuyến AB,AC với đường tròn (B , C là các tiếp điểm ) a, Chứng minh tứ giác ABOC là tứ giác nội tiếp b, Cho bán kính đường tròn (O) bằng 3cm , độ dài đoạn thẳng OA bằng 5cm .Tính độ dài đoạn thẳng BC
Cho điểm A nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến AB, AC với (O) (B và C là các tiếp điểm). Vẽ đường kính CE của (O). Gọi H là giao điểm của OA và BC. a) Chứng minh tứ giác ABOC nội tiếp và BE // OA. b) AE cắt (O) tại D (khác E), BD cắt OA tại M. Chứng minh MAD MBA vàAH AC D D . c) Vẽ EI vuông góc với OA tại I; vẽ DK là đường kính của (O). Chứng minh 3 điểm K, I, B thẳng hàng.
a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên AO là trung trực của BC
=>AO vuông góc BC
góc EBC=1/2*180=90 độ
=>EB vuông góc BC
=>AO//EB
b: Xét ΔMAD và ΔMBA co
góc AMD chung
góc MDA=góc MAB
=>ΔMAD đồng dạng với ΔMBA
(Quảng Ninh - 2020)
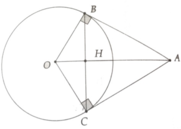
Cho đường tròn $(O; R)$ và $A$ là một điểm nằm bên ngoài đường tròn. Từ điểm $A$ kẻ hai tiếp tuyến $AB$ và $AC$ với đường tròn $(O)$ ($B$ và $C$ là hai tiếp điểm). Gọi $H$ là giao điểm của $AO$ và $BC$. Kẻ đường kính $BD$ của đường tròn $(O)$, $AD$ cắt đường tròn tại điểm thứ hai là $E$.
a. Chứng minh $ABOC$ là tứ giác nội tiếp.
b. Tính độ dài $AH$, biết $R = 3$cm, $AB = 4$cm.
c. Chứng minh $AE.AD = AH.AO$.
d. Tia $CE$ cắt $AH$ tại $F$. Chứng tỏ $F$ là trung điểm của $AH$.
a. Ta có: \(\Lambda\)ABO=90 ( do AB là tiếp tuyến của (O))
\(\Lambda\)ACO=90 ( do AC là tiếp tuyến của (O))
\(\Rightarrow\) \(\Lambda\)ABO + \(\Lambda\)ACO = 90 + 90 = 180.
Suy ra: tứ giác ABOC nội tiếp.
b. Ta có: AB,AC lần lượt là tiếp tuyến của (O) nên AB=AC.
\(\Rightarrow\)\(\Delta\)ABC cân tại A lại có AH là tia phân giác nên AH cũng là đường cao
\(\Rightarrow\)AO\(\perp\)BC tại H.
Áp dụng đinh lý Py-ta-go vào \(\Delta\)ABO ta có:
AO2 = AB2 + BO2 = 42 + 32 = 25
\(\Rightarrow\)AO = 5 (cm).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ABO ta được:
AB2 = AH.AO \(\Rightarrow\) AH = \(\dfrac{AB^2}{AO}\)=\(\dfrac{16}{5}\)(cm)
c. Ta có: \(\Lambda\)ACE=\(\Lambda\)ADC ( tính chất của góc tạo bởi tia tiếp tuyến và dây cung )
Xét \(\Delta\)ACE và \(\Delta\)ADC có:
\(\Lambda ACE=\Lambda ADC\)
\(\Lambda\)CAD chung
Do đó: \(\Delta ACE\sim\Delta ADC\) \(\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AC}\) \(\Rightarrow\)AC2 = AD.AE (1)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ACO có:
AC2 = AH.AO (2)
Từ (1) và (2) ,suy ra: AD.AE = AH.AO.
a)Ta có:\(\widehat{ABO};\widehat{ACO}\) lần lượt là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ABO=}\widehat{ACO}=90^{ }\)
\(\Rightarrow\widehat{ABO}+\widehat{ACO}=90+90=180\)
Mà hai góc này đối nhau nên tứ giác ABOC nội tiếb)
b)Theo a) ta có:\(\widehat{ABO}=90\)⇒▲ABO là tam giác vuông tại B đường cao AH.
Áp dụng định lí pytago vào tam giác vuông ABO đường cao AH ta có:
\(AO^2=AB^2+BO^2=4^2+3^2=25\)
\(\Rightarrow\sqrt{AO}=5\) cm.
Áp dụng hệ thức lượng giữa cạnh và đường cao trong ▲vuông ABO ta có:
\(AB^2=AH\cdot AO\)
\(\Rightarrow AH=\dfrac{AB^2^{ }}{AO}=\dfrac{4^2^{ }}{5}=\dfrac{16}{5}\)