Kẻ DE//AB. BD/CD = AE/EC = AB/AC => AE/(EC+AE) = AB/(AB+AC) <=> AE = 10

^BAD = ^ADE  (so le trong) => T/g ADE cân tại E

Kẻ EH vuông góc với AD => AH = 1/2 AD = 6. Theo đ/l Py-ta-go tính được EH = 8

=> S(ADE) = 48

S(ADE)/S(ADC) = AE/AC = 5/7 => S(ADC) = 67,2

S(ABD)/S(ADC) = BD/CD = 35/14 = 5/2 => S(ABD) = 168 

=> S(ABC) = 235,2 (cm^2)

10/35 mà = 5/7

bạn trên làm sai rồi

Kẻ DE//AB. BD/CD = AE/EC = AB/AC => AE/(EC+AE) = AB/(AB+AC) <=> AE = 10

^BAD = ^ADE  (so le trong) => T/g ADE cân tại E

Kẻ EH vuông góc với AD => AH = 1/2 AD = 6. Theo đ/l Py-ta-go tính được EH = 8

=> S(ADE) = 48

S(ADE)/S(ADC) = AE/AC = 5/7 => S(ADC) = 67,2

S(ABD)/S(ADC) = BD/CD = 35/14 = 5/2 => S(ABD) = 168 

=> S(ABC) = 235,2 (cm^2)

lám sao ra 235,2 vậy bạn nào chỉ mình voi

Vẽ DE//AB suy ra tam giác AED cân tại E suy ra EA = ED

Mặt khác DE/AB = CE/AC suy ra DE.AC = AB.CE suy ra 35DE = 14CE suy ra 35DE = 14 ( 35 - AE ) mà ( AE = DE ) 

suy ra 35DE = 14( 35-DE) suy ra DE = 10 suy ra AE = 10 suy ra CE = 25

Vẽ EK vuông góc vs AD dễ dàng tính được EK = 8 suy ra diện tích ADE = 48

Đến đay bn tự suy ra S abc nhé

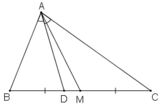
a) Ta có: 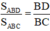 (do hai tam giác có chung chiều cao từ đỉnh A)

ΔABC có AD là phân giác

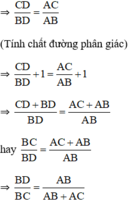
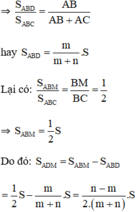
b) Với n = 7; m = 3, thay vào kết quả phần a ta có:

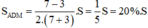
Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.

a:

Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=15^2+20^2=625\)

=>\(BC=\sqrt{625}=25\left(cm\right)\)

Ta có: ΔABC vuông tại A

=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot15\cdot20=150\left(cm^2\right)\)

Xét ΔABC có AD là phân giác

nên \(\dfrac{BD}{CD}=\dfrac{AB}{AC}\)

=>\(\dfrac{BD}{CD}=\dfrac{3}{4}\)
=>\(\dfrac{CD}{BD}=\dfrac{4}{3}\)

=>\(\dfrac{CD+BD}{BD}=\dfrac{4+3}{3}\)

=>\(\dfrac{BC}{BD}=\dfrac{7}{3}\)

=>\(BD=\dfrac{3}{7}BC\)

=>\(S_{ABD}=\dfrac{3}{7}\cdot S_{ABC}\)

b: Vì I là trung điểm của BC

nên \(S_{ABI}=\dfrac{1}{2}\cdot S_{ABC}\)

=>\(\dfrac{S_{ABD}}{S_{ABI}}=\dfrac{3}{7}:\dfrac{1}{2}=\dfrac{6}{7}\)

c: \(S_{ABD}=\dfrac{3}{7}\cdot S_{ABC}=\dfrac{3}{7}\cdot140=60\left(cm^2\right)\)

\(S_{ABI}=\dfrac{7}{6}\cdot S_{ABD}=\dfrac{7}{6}\cdot60=70\left(cm^2\right)\)

ta có: \(S_{ABD}+S_{AID}=S_{ABI}\)

=>\(S_{AID}+60=70\)

=>\(S_{AID}=10\left(cm^2\right)\)

a: \(AC=\sqrt{12^2+14^2}=2\sqrt{85}\left(cm\right)\)

\(BH=\dfrac{BA\cdot BC}{AC}=\dfrac{12\cdot14}{2\sqrt{85}}=\dfrac{84\sqrt{85}}{85}\left(cm\right)\)

b: Xét ΔABC có BD là đường phân giác

nên AD/AB=CD/BC

=>AD/12=CD/14

=>AD/6=CD/7

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AD}{6}=\dfrac{CD}{7}=\dfrac{AD+CD}{6+7}=\dfrac{2\sqrt{85}}{13}\)

Do đó: \(AD=\dfrac{12\sqrt{85}}{13}\left(cm\right);CD=\dfrac{14\sqrt{85}}{13}\left(cm\right)\)