CHO TỨ GIÁC ABCD CÓ GÓC DAC =GÓC DBC CMR
AB.DC+AD.BC=AC.BD
cho tứ giác lồi ABCD có góc b = góc d =90 độ ,trên đường chéo ac lấy e sao cho góc abe=góc dbc, gọi I là trung điểm AC biết góc BAC=góc BDC,góc CBD=góc CAD.CM: a,góc BIC=2BDC,góc CID=2CBD b,Tam giác ABE ~ DBC c,AC.BD=AB.DC+AD.BC
1,cho tứ giác lồi ABCD có góc b = góc d =90 độ ,trên đường chéo ac lấy e sao cho góc abe=góc dbc, gọi I là trung điểm AC biết góc BAC=góc BDC,góc CBD=góc CAD.CM:
a,góc BIC=2BDC,góc CID=2CBD
b,Tam giác ABE ~ DBC
c,AC.BD=AB.DC+AD.BC
2.cho tam giác ABC;H,G,O lần lượt là trực tâm ,trọng tâm,giao điểm 3 đường trung trực,gọi E,D là trung điểm AB,Ac
a,CM:tam giác OED ~ HCB
b,tam giác GOP ~ GHP
3.cho hbh ABCD có AC>BD,gọi H,K lần lượt là hình chiếu vuông góc của c trên AD,AB
a,CH/CB=CK/CD
b,tam giác CHK ~ BCA
c,AB.AH+AD.AK=AC^2
Cho tứ giác lồi ABCD có Góc B = Góc D = 90độ .
Đường chéo AC lấy E , góc ABE = góc DBC
I là trung điểm của AC.
Biết góc BAC = góc BDC , góc CBD = góc CAD
a. Cm: Góc BIC = 2 lần góc BDC
Góc CID = 2 lần góc CBD
b. Cm: Tam giác ABE đồng dạng với Tam giác DBC
c. Cm: AC.BD = AB.CD + AD.BC
cho tứ giác ABCD có: góc DAC = góc DBC = 90 độ. cmr:
a) góc ADB = góc ACB
b) góc ABD = góc ACD
Cho tứ giác \(ABCD\) có \(AB=BD=BC.\) Có góc \(DBC\) = 36 độ, góc DAC = ?
Góc DAC = (360-36x2):2= 144 độ
Đáp số 144 độ
cho tứ giác ABCD có AB=BD=BC , góc DBC =76 độ . Tính góc DAC
cho tứ giác ABCD có góc A và góc C vuông. gọi O là giao điểm của AC và BD, I là giao điểm của AB và CD.
a) CMR: IA.ID=IC.IB
b) CMR \(\widehat{ADB}=\widehat{ACB}\)
c)CM: AD.BC+AB.CD=AC.BD
Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD. Chứng minh AD.BC=AC.BD
AD/AC=DE/EC
DB/BC=DE/EC
=>AD/AC=DB/BC
=>AD*BC=DB*AC
Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD. Chứng minh AD.BC=AC.BD
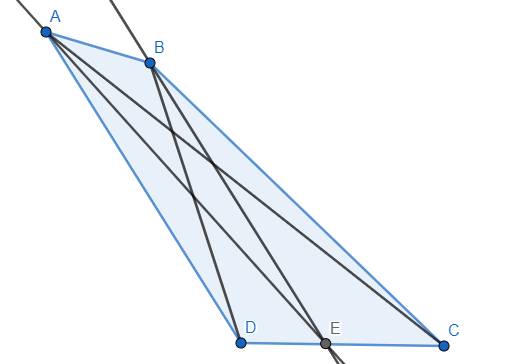
Áp dụng tính chất tia phân giác, ta có \(\dfrac{ED}{EC}=\dfrac{AD}{AC}\) và \(\dfrac{ED}{EC}=\dfrac{BD}{BC}\). Từ đó suy ra \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow AD.BC=AC.BD\) (đpcm)