AD/AC=DE/EC
DB/BC=DE/EC
=>AD/AC=DB/BC
=>AD*BC=DB*AC
AD/AC=DE/EC
DB/BC=DE/EC
=>AD/AC=DB/BC
=>AD*BC=DB*AC
Cho tam giác ABC có BC < BA, đường phân giác BE và trung tuyến BD ( E và D thuộc AC). Đường thẳng vuông góc với BE kẻ từ C cắt BE,BD tại F và G. Chứng minh rằng:a)GE//BCb)DF đi qua trung điểm của GE
cho ABCD là hình thang cân (AB//CD,AB<CD,góc ADC=60 độ),đường phân giác của góc ADC cắt AC,AB lần lượt tại I,M.Kẻ AE//BC(E thuộc DC).
a) chứng minh tam giác ADE là tam giác đều và DC=AB+AM.
b)Cho IA/IC=4/11 và MA-MB=6cm.Tính MB/AM và AM,MB.
Cho△ MNP , trung tuyến MD . Tia phân giác của góc MDN cắt cạnh MN tại E , tia phân giác của góc MDP cắt cạnh MP tại F
a, Chứng minh : EF//NP
b, Chứng minh : G là trung điểm của EF
giải thích hộ mik cách làm lun nhé , mik cảm ơn nhìu nhìu nhìu :)))
Bài 3:Cho tam giác ABC với trung tuyến AM.Tia phân giác góc AMB cắt cạnh AB tại D,tia phân giác góc AMC cắt cạnh AC tại E.
a)Chứng minh DE và BC song song với nhau.
b)Gọi I là giao điểm của AM,DE.Chứng minh IM=\(\dfrac{1}{2}\)DE.
cho tam giác ABC, đường cao AD. gọi M, N theo thứ tự là các điểm đối xứng của D qua các cạnh AB, AC và E,F theo thứ tự là giao điểm của MN với AB và AC. C/m AD là phân giác của góc EDF
Cho tam giác ABC có AB > AC, BE là phân giác, BD là trung tuyến (E,D thuộc cạnh AC). Đường thẳng qua C vuông góc với BE cắt BE, BD, BA lần lượt tại F, G và K. DF cắt BC tại M. Chứng minh rằng
a) M là trung điểm của đoạn thẳng BC.
b)DA/DE=1+BK/DF
Cho tam giác ABC(AB<AC), AD là phân giác trong của góc A. Qua trung điểm E của cạnh BC, vẽ đường thẳng song song với AD, cắt cạnh AC tại F, cắt đường thẳng AB tại G. Chứng minh CF=BG
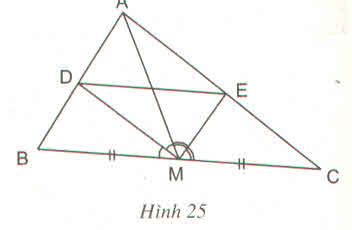
Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC (h.25)
Cho tam giác MNP trung tuyến ME. Các đường phân giác của góc MEN và góc PEM lần lượt cắt các cạnh MN, MP tại C và D a) cmr: CD // NP b) gọi O là giao điểm của ME và CD. Cmr OC= OD