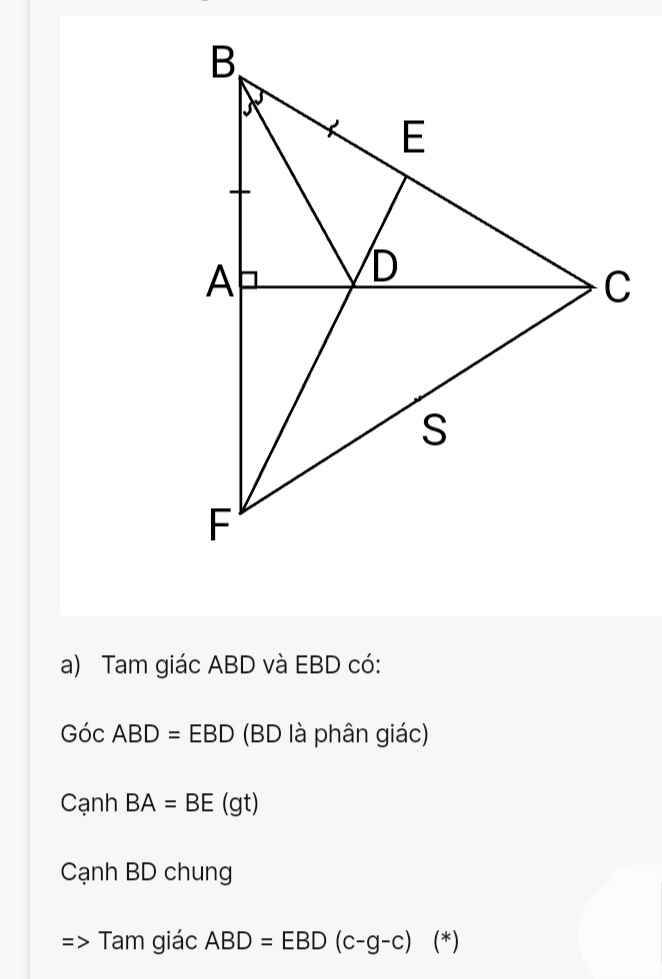
Bài:Cho tam giác ABC vuông tại A có AB=3cm,AC=4cm.
a)Vẽ BD là tia phân giác của góc ABC,kẻ DE vuông góc với BC(E thuộc BC).Chứng minh:DA=DE
b)Gọi giao điểm BD và AE là H.Chứng minh:BH vuông góc AE tại H
c)Tính độ dài BC
d)Trên tia đối của tia DE lấy điểm F sao cho DC=DF.Chứng minh :3 điểm A,B,F thẳng hàng.
GIải giúp mình với."Mình đang cần gấp"