
Những câu hỏi liên quan
Bài 1:cho hình thoi ABCD có góc B =60 . kẻ AE vuông góc DC,AF vuông góc BC.
a. CM AE=AF
b. CM tam giác AEF đều
c. Biết BD =16cm. Tính chu vi tam giác AEF
Bài 2:
Cho hình thoi ABCD có góc A =60. Vẽ BH vuông góc AD rồi kéo dài 1 đoạn HE =HB
a.CM ABDE là hình thoi
b.3 điểm E,D,C thẳng hàng
c. Cm EB=AC
mình cần gấp cảm ơn
a: Xét ΔABD có AB=AD và góc BAD=60 độ
nên ΔABD đều
=>BD=AB
Xét tứ giác ABDE có
H là trung điểm chung của AD và BE
AB=BD
=>ABDE là hình thoi
b: ABDE là hình thoi
=>DE//AB
mà DC//AB
nên D,E,C thẳng hàng
Đúng 1
Bình luận (0)
Cho hình thoi ABCD có BC = 6 cm. Chu vi hình thoi ABCD là
chu vi hình thoi ABCD là
6 . 4 = 24 ( cm )
Đúng 1
Bình luận (0)
a) Cho hình thoi ABCD. Kẻ hai đường cao AH, AK. Chứng minh rằng AH = AK ?
b) Hình bình hành ABCD có hai đường cao AH, AK bằng nhau. Chứng minh rằng ABCD là hình thoi ?
Giải:
a) Hình vẽ:
Xét hai tam giác vuông \(AHD\) và \(AKB\) ta có:
\(AD=AB\) (cạnh hình thoi)
\(\widehat{D}=\widehat{B}\) (hai góc đối hình thoi)
Do đó: \(\Delta AHD=\Delta AKB\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=AK\) (Đpcm)
b) Hình vẽ:
Cách 1: Ta có: \(\Delta AHD=\Delta AKB\left(g.c.g\right)\)
\(\Rightarrow AD=AK\)
Hình bình hành \(ABCD\) có hai cạnh kề bằng nhau nên là hình thoi (Đpcm)
Cách 2: Ta có: \(\Delta AHC=\Delta AKC\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\)
Hình bình hành \(ABCD\) có một đường chéo là phân giác của một góc nên là hình thoi (Đpcm)
Đúng 0
Bình luận (1)
Cho hình thoi ABCD có chu vi là 48cm . Độ dài cạnh hình thoi ABCD là:
Cho hình thoi ABCD có AC = BD . Tìm tâm đường tròn ngoại tiếp hình thoi ABCD ?
A. Điểm A.
B. Giao điểm của AC và BD
C. Không có đường tròn ngoại tiếp tứ giác ABCD.
D. Trung điểm cạnh AB.
Đáp án B
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
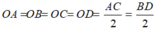
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Đúng 0
Bình luận (0)
Có ai biết làm bài này hông ?
Cho hình thoi ABCD có BC = 8cm, chiều cao AH = 5cm. Tính diện tích
hình thoi ABCD (hình thoi được coi là hình bình hành) ![]()
Diện tích hình thoi ABCD là:
\(8\times5:2=20\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Diện tích hình thoi `ABCD` là:
`8xx5:2=20(cm^2)`
Đáp só: `20 \ cm^2`
Đúng 1
Bình luận (0)
Diện Tích hình thoi ABCD là : \(8 \) x \(5 : 2 = 20 \) [ cm2 ]
Đúng 1
Bình luận (0)
a) cho hình thoi ABCD . kẻ hai đường cao AH , AK . Chứng minh rằng AH=AK
b) hình bình hành ABCD có hai đường cao AH,AK bằng nhau . Chứng minh rằng ABCD là hình thoi
a,xét 2 tan giác vuông ABH và AKD có:
^H=^K=90ĐỘ
ab=ad(GT)
^B=^D(T/C hình thoi)
=>tam giác AHB=tam giác AKD( cạnh huyền-góc nhọn)
=>AH=AK
b,ta có:^a1+^a2=90độ (tổng 2 góc nhọn trong tam giác vuông)
^a2+^b=90độ(như trên)
mà ^d=^b( 2 góc đối)
=>^a1=^a2
xét tam giác ADH và ABK có:
^a1=^a2(cmt)
AH=AK(gt)
^h=^k=90độ
=>tam giác ADH=ABK(g.c.g)=>AD=AB(tương ứng)
-hình bình hành có 2 cạnh liên tiếp AD=AB
=>ABCD là hình thoi
=>
Đúng 0
Bình luận (0)
xét \(\Delta\)ACK và ABH có
AB=AC(tc hình thoi)
\(\widehat{AKC}=\widehat{AHB}=90^o\)
\(\widehat{B}=\widehat{C}\)
theo trường hợp cạnh huyền góc nhọn
=>AH=AK (2 cạnh tương ứng)
b)
xét \(\Delta\)AKDvà \(\Delta\)AHB
có\(\widehat{AHB}=\widehat{AK\text{D}}=90^o\)
AH=AK(gt)
\(\widehat{B}=\widehat{D}\)(tính chất HBH)
=>AB=AD(2 cạnh tương ứng)
ABCD là hình thoi vì là HBH có 2 cạnh kề bằng nhau
Đúng 0
Bình luận (0)
Viết vào chỗ chấm cho thích hợp:
Hình ABCD là hình thoi có: c) Diện tích hình thoi ABCD là…
1.Cho hình thoi ABCD có cạnh =a.Biết góc B=60 độ
a)C/m tam giác ABC đều
b)Tính diện tích hình thoi ABCD theo a
2.Cho hình vuông ABCD có độ dài cạnh =a.Điểm M bất kì trên đường thẳng AC.Kẻ ME vuông góc AB tại E và MF vuông góc AC tại F.Tìm vị trí của điểm M trên AC để diện tích tam giác CEF lớn nhất
1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)
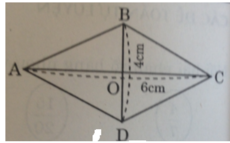
Cho hình thoi ABCD có AC=8cm, BD=6cm. Tính chu vi hình thoi ABCD
Gọi \(O\) là giao điểm của \(AC\)và \(BD\).
Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)
Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)
Áp dụng định lí Pitago trong \(\Delta AOB\) có:
\(AB^2=AO^2+OB^2\)
\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)
\(\Rightarrow AB=5cm\)
\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)
Vậy ...............





























