Cho tam giác ABC có AB = AC và H là trung điểm của BC
a) Chứng minh: ΔABH = ΔACH;
b) Chứng minh: AH ⊥ BC;
c) Vẽ HD ⊥ AB (D ∈ AB) và HE ⊥ AC (E ∈ AC). Chứng minh: ΔBDH = ΔCEH.
cho ΔABC có AB = AC = 10cm, BC = 12cm. Kẻ AH ⊥BC tại H
a) Chứng minh rằng: ΔABH = ΔACH. Từ đó suy ra H là trung điểm của BC
b) Tính độ dài AH
c) Kẻ HI ⊥ AB tại I và HK ⊥ AC tại K. Vẽ các điểm D và E sao cho I, K lần lượt là trung điểm của HD và HE. Chứng minh rằng AE = AH
d) Tam giác ADE là hình gì? Vì sao? Chứng minh DE // BC
e) Tìm điều kiện của tam giác abc để a là trung điểm của de
Cho tam giác ABC cân tại A, AB > BC, H là trung điểm của BC
a) Chứng minh: ΔABH = ΔACH. Từ đó suy ra AH vuông góc với BC
b) Tính độ dài AH nếu BC = 4cm; AB = 6cm
c) Tia phân giác của góc B cắt AH tại I. Chứng minh tam giác BIC cân
d) Đường thẳng đi qua a song song với BC cắt BI và CI tại M và N. Chứng minh A là trung điểm của MN
đề có sai không zợ
nói tg ABC cân mà AB>AC
a)\(\text{ Xét }\Delta ABH\)\(\text{và }\Delta ACH\)\(\text{có}\)
\(AB=AC\)
\(\widehat{ABH}=\widehat{ACH}\left(\Delta\text{ABC cân}\right)\)
\(BH=CH\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}\)
\(\text{Mà }\widehat{AHB}+\widehat{AHC}=180^o\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^o\)
\(\Rightarrow AH\perp BC\)
b) \(\text{Có }BH=\frac{BC}{2}\left(gt\right)\)
\(\text{Mà BC = 4 ( GT )}\)
\(\Rightarrow BH=4cm\)
\(\text{Áp dụng định lý Py-ta-go vào tam giác ABH vuông tại H ta được :}\)
\(\text{AH^2 + BH^2 = AB^2}\)
\(\Rightarrow AH^2+2^2=6^2\)
\(\text{=> AH^2 = 32}\Rightarrow AH^2=32\)\(\Rightarrow AH^2=32\)
\(\Rightarrow AH=\sqrt{32}\)
\(\text{Vậy }AH=\sqrt{32}\)
cho tam giác ABC có AB=AC.Lấy điểm H là trung điểm cạnh BC.
a)Chứng minh ΔABH=ΔACH,từ đó suy ra : góc B= góc C
b)Tính số đo góc AHB
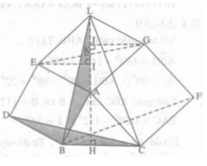
Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC cho trước. Gọi H là điểm thuộc đường thẳng BC sao cho AH ⊥ BC. Gọi I, J là các điểm thuộc đường thẳng AH sao cho EI ⊥ AH và GJ ⊥ AH. Chứng minh
ΔABH = ΔEAI, ΔACH = ΔGAJ
Từ đó suy ra đường thẳng AH cắt EG tại trung điểm K của EG (tức là AK là trung tuyến của tam giác AEG)
+) Xét tam giác EIA vuông tại I nên :
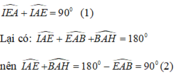
+) Xét hai tam giác ABH và ∆EAI có:
AB = AE ( vì ABDE là hình vuông)
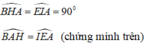
Suy ra: ∆ABH = ∆ EAI ( cạnh huyền – góc nhọn)
⇒ AH = EI ( hai cạnh tương ứng)
+) Tương tự hai tam giác vuông ACH và GAJ bằng nhau.
⇒ AH = GJ.
Suy ra EI = AH = GJ.
+) Xét ΔEKI và ΔGKJ có:
EI = GJ ( chứng minh trên)
∠(IKE) = ∠(JKG) (đối đỉnh).
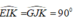
do đó ΔEKI = ΔGKJ ( cgv – gn)
suy ra: KE = KG
Từ đó ta có K trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.
Cho tam giác ABC có AB = AC. Gọi H là trung điểm của BC.
a) Chứng minh ΔABH = ΔACH
b) Vẽ HI⊥AB tại I và vẽ HK⊥AC tại K. Chứng minh AI = AK
c) Chứng minh IK // BC
d) Gọi M là trung điểm IK. Chứng minh A, M, H thẳng hàng.
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
DO đó: ΔAHB=ΔAHC
Cho ΔABC cân tại A, biết AB = 5cm, BC = 6cm. Gọi H là trung điểm của BC.
a) Chứng minh: ΔABH = ΔACH
b) Chứng minh: AH ⊥ BC
c) Tính AH
d) Kẻ HE ⊥ AB (E ∈ AB), HK ⊥ AC (K ∈ AC). Chứng minh: HE = HK
e) Chứng minh: EK // BC
Ai giúp mik vs !!
a) Xét tam giác ABH và tam giác ACH có
AB=AC (tam giác ABC cân tại A)
\(\widehat{ABH}=\widehat{ACH}\)(tam giác ABC cân tại A)
BH=HC(H là trung điểm BC)
=> Tam giác ABH = Tam giác ACH (cgc)
b) Vì tam giác ABC cân tại A (gt) và H là trung điểm BC(gt)
=> AH là đường trung tuyến đồng thời là đường cao của tam giác ABC
=> AH vuông góc với BC(đpcm)
a) Xét t/giác ABH và t/giác ACH
c: AB = AC (gt)
BH = CH (gt)
AH: chung
=> t/giác ABH = t/giác ACH (c.c.c)
b) Ta có: t/giác ABH = t/giác ACH (cmt)
=> \(\widehat{AHB}=\widehat{AHC}\)(2 góc t/ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(kề bù)
=> \(\widehat{AHB}=\widehat{AHC}=90^0\)
=> AH \(\perp\)BC
c) Ta có: BH = CH = 1/BC = 1/2.6 = 3 (cm)
Áp dụng định lí Pi - ta - go vào t/giác ABH vuông tại H, ta có:
AB2 = AH2 + BH2 => AH2 = 52 - 32 = 16
=> AH = 4 (cm)
d) Ta có: t/giác AHB = t/giác AHC (cmt)
=> \(\widehat{A_1}=\widehat{A_2}\) (2 góc t/ứng)
Xét t/giác AHE và t/giác AHK
có: \(\widehat{A_1}=\widehat{A_2}\)(cmt)
AH : chung
\(\widehat{AEH}=\widehat{AKH}=90^0\)(gt)
=> t/giác AHE = t/giác AHK (ch - gn)
=> HE = HK (2 cạnh t/ứng)
e) Ta có: t/giác AHE = t/giác AHK (cmt)
=> AE = AK (2 cạnh t/ứng)
=> t/giác AEK cân tại A
=> \(\widehat{AEK}=\widehat{AKE}=\frac{180^0-\widehat{A}}{2}\)(1)
T/giác ABC cân tại A
=> \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AEK}=\widehat{B}\)
Mà 2 góc này ở vị trí đồng vị
=> EK // BC
Bài 1: Cho 2 tam giác vuông, ΔABC vuông tại A, MNP vuông tại M. Biết ΔABC = ΔMNP, AB= 20cm, AC= 15cm. Tính các cạnh của ΔMNP
Bài 2: Cho ΔABC có AB=AC. Gọi H là trung điểm của cạnh BC a) Chứng minh ΔABH = ΔACH b) Chứng minh AH vuông ∠ BC c) Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Chứng minh ΔHAD = ΔHAE d) Gọi K là trung điểm của DE. Chứng minh 3 điểm A, H, K thẳng hàng
ANH CHỊ GIÚP EM VỚI CHIỀU EM NỘP RỒI
Cho tam giác ABC có 3 góc đều nhọn, AB < AC. Vẽ AH vuông góc với BC (H thuộc BC). Trên tia AH lấy điểm K sao cho H là trung điểm của AK.
a) Chứng minh rằng ΔACH=ΔKCH
b) Gọi E là trung điểm BC. Trên tia AE lấy điểm D sao cho E là trung điểm của AD. Chứng minh rằng BD =CK.
c) Chứng minh EH là phân giác của góc AEK và DK∥BC
d) Gọi I là giao điểm của BD là CK, N là trung điểm của KD. Chứng minh ba điểm E, I, N thẳng hàng.
a, xét tam giác ACH và tam giác KCH có : CH chung
góc AHC = góc KHC = 90
AH = HK do H là trđ của AK (gt)
=> tam giác ACH = tam giác KCH (2cgv)
b, xét tam giác AEC và tam giác DEB có : góc BED = góc CEA (đối đỉnh)
BE= EC do E là trđ của BC (GT)
AE = ED do E là trđ của AD (gt)
=> tam giác AEC = tam giác DEB (c-g-c)
=> BD = AC (đn)
tam giác ACH = tam giác KCH (câu a) => AC = CK (đn)
=> BD = CK (tcbc)
c, xét tam giác AEH và tam giác KEH có: EH chung
AH = HK (câu a)
góc AHE = góc KHE = 90
=> tam giác AEH = tam giác KEH (2cgv)
=> góc AEH = góc KEH mà EH nằm giữa EA và EK
=> EH là phân giác của góc AEK (đn)
Cho ΔABC cân tại A, trung tuyến AK. Gọi H là điểm nằm giữa A và K, chứng minh rằng:
a) ΔABK = ΔACK; ΔABH = ΔACH
b) ΔBHC cân
c) Cho AB = 5cm, BC = 6cm. Tính AK
bài này khá dễ, hình em tự vẽ nhé
a. Xét 2 tg ABK và ACK có:
AK chung
góc AKB = góc AKC ( đều = 900)
BK=CK ( vì AK là trung tuyến)
=> ABK = ACK ( 2 cạnh góc vuông)
Ta có: trong tam giác ABC cân, AK vừa là đường trung tuyến vừa là đg phân giác
=> góc BAH = góc CAH
Xét tg ABH và ACH
AH chung
góc BAH = CAH
BC = AC ( vì tg ABC chung)
=> tg ABH = ACH ( c.g.c)
b. theo a, ta có: tg ABH = tg ACH (cgc)
=> góc ABH = góc ACH
Mà theo gt góc ABC = góc ACB => HBC = HCB
=> tg BHC cân tại H
c. Vì AK là đg trung tuyến của tg ABC
=> BK = KC = BC / 2 = 6/3 = 2
Vậy BK = 2 cm
Xét tg ABK
Theo định lí Py- ta- go ta có:
AK ^ 2 + BK ^ 2 = AB ^ 2
hay AK^2 + 2^2 = 5^2
AK^2 + 4 = 25
AK^2 = 25- 4
AK^2= 21
=> AK = căn 21
cho tam giác ABC (AB<AC), tia phân giác AD (D thuộc BC). Vẽ BE vuông AD (E thuộc AC) và H là giao điểm của AD và BE.
a, chứng minh ΔABH = ΔAEH
b, chứng minh tam giác BDE là tam giác cân
c, Trên tia đối của DE lấy K sao cho DC = DK. Chứng minh góc KBD = góc CED và A, B, K thẳng hàng
d, Chứng minh BE // KC
a: Xét ΔAHB vuông tại H và ΔAHE vuông tại H có
AH chung
\(\widehat{BAH}=\widehat{EAH}\)
Do đó: ΔAHB=ΔAHE
b:
Ta có: ΔAHB=ΔAHE
=>AB=AE
Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE
=>ΔDBE cân tại D
c: Xét ΔBDK và ΔEDC có
DB=DE
\(\widehat{BDK}=\widehat{EDC}\)
DK=DC
Do đó: ΔBDK=ΔEDC
=>\(\widehat{KBD}=\widehat{CED}\)
Ta có: ΔBAD=ΔEAD
=>\(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{KBD}\)
\(=\widehat{AED}+\widehat{CED}\)
\(=180^0\)
=>A,B,K thẳng hàng
d: Ta có: ΔDBK=ΔDEC
=>BK=EC
Xét ΔADC có \(\dfrac{AB}{BK}=\dfrac{AE}{EC}\)
nên BE//KC