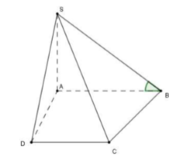
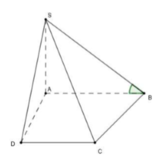
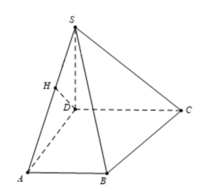
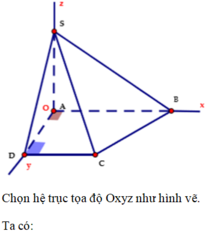
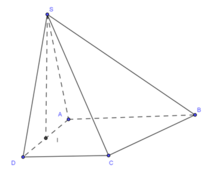
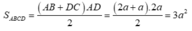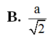Hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; biết AB = AD = 2a, CD = a. Gọi I là trung điểm của AD, biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD), Thể tích khối chóp S.ABCD bằng 3 15 a 3 5 . Góc giữa hai mặt phẳng (SBC) và (ABcD) bằng
A . 90 0
B . 60 0
C . 30 0
D . 45 0