Các câu hỏi tương tự
Cho hình chóp S.ABCD có
S
A
⊥
A
B
C
D
và đáy ABCD là hình vuông. Từ A kẻ
A
M
⊥
S
B
. Khẳng định nào sau đây đúng? A.
A
M
⊥
S
B
D
B.
A
M
⊥
S
B...
Đọc tiếp
Cho hình chóp S.ABCD có S A ⊥ A B C D và đáy ABCD là hình vuông. Từ A kẻ A M ⊥ S B . Khẳng định nào sau đây đúng?
A. A M ⊥ S B D
B. A M ⊥ S B C
C. S B ⊥ M A C
D. A M ⊥ S A D
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Gọi E; F lần lượt là hình chiếu của A lên SB, SD. Khẳng định nào sau đây đúng?
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Gọi E; F lần lượt là hình chiếu của A lên SB, SD. Khẳng định nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy, I là tâm mặt cầu ngoại tiếp hình chóp. Khẳng định nào sau đây là đúng? A. I là trung điểm SC B. I là tâm đường tròn ngoại tiếp tam giác SBD C. I là giao điểm của AC và BD D. I là trung điểm SA.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy, I là tâm mặt cầu ngoại tiếp hình chóp. Khẳng định nào sau đây là đúng?
A. I là trung điểm SC
B. I là tâm đường tròn ngoại tiếp tam giác SBD
C. I là giao điểm của AC và BD
D. I là trung điểm SA.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy, I là tâm mặt cầu ngoại tiếp hình chóp. Khẳng định nào sau đây là đúng? A. I là trung điểm SC B. I là tâm đường tròn ngoại tiếp tam giác SBD C. I là giao điểm của AC và BD D. I là trung điểm SA
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy, I là tâm mặt cầu ngoại tiếp hình chóp. Khẳng định nào sau đây là đúng?
A. I là trung điểm SC
B. I là tâm đường tròn ngoại tiếp tam giác SBD
C. I là giao điểm của AC và BD
D. I là trung điểm SA
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, SA vuông góc với đáy ABCD. Gọi I là trung điểm của SC. Xét các khẳng định sau: Trong các khẳng định trên, có tất cả bao nhiêu khẳng định ĐÚNG ? A. 3 B. 1 C. 4 D. 2
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, SA vuông góc với đáy ABCD. Gọi I là trung điểm của SC. Xét các khẳng định sau:
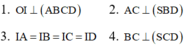
Trong các khẳng định trên, có tất cả bao nhiêu khẳng định ĐÚNG ?
A. 3
B. 1
C. 4
D. 2
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. M là điểm thuộc cạnh SD. Khẳng định nào sau đây là đúng? A. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC cắt nhau. B. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC chéo nhau. C. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng BD cắt nhau. D. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC song song với nhau.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. M là điểm thuộc cạnh SD. Khẳng định nào sau đây là đúng?
A. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC cắt nhau.
B. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC chéo nhau.
C. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng BD cắt nhau.
D. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC song song với nhau.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây đúng?
A. d qua S và song song với BC.
B. d qua S và song song với DC.
C. d qua S và song song với AB.
D. d qua S và song song với BD.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của 2 đường chéo và SA SC. Các khẳng định sau, khẳng định nào đúng? A.
S
A
⊥
A
B
C
D
B.
B
D
⊥
S
A
C
C.
A
C
⊥
S
B
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của 2 đường chéo và SA = SC. Các khẳng định sau, khẳng định nào đúng?
A. S A ⊥ A B C D
B. B D ⊥ S A C
C. A C ⊥ S B D
D. A B ⊥ S A C
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết AB2a, ADDCa. Cạnh bên SA vuông góc với đáy và SAasqrt{2}. CHọn khẳng định sai?A: widehat{left(SBCright);left(ABCDright)}45^0B: widehat{left(SDCright);left(BCDright)}60^0C: Giao tuyến của (SAB) với (SCD) song song ABD: left(SBCright)perpleft(SACright)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết AB=2a, AD=DC=a. Cạnh bên SA vuông góc với đáy và \(SA=a\sqrt{2}\). CHọn khẳng định sai?
A: \(\widehat{\left(SBC\right);\left(ABCD\right)}=45^0\)
B: \(\widehat{\left(SDC\right);\left(BCD\right)}=60^0\)
C: Giao tuyến của (SAB) với (SCD) song song AB
D: \(\left(SBC\right)\perp\left(SAC\right)\)






