Chọn A.
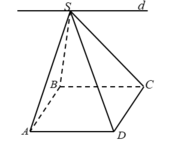
- Xét 2mp (SAD) và (SBC) có: Điểm S chung:
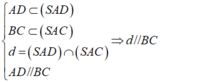
(Theo hệ quả của định lý 2 (Giao tuyến của ba mặt phẳng)).
Chọn A.

- Xét 2mp (SAD) và (SBC) có: Điểm S chung:
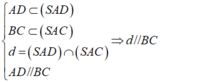
(Theo hệ quả của định lý 2 (Giao tuyến của ba mặt phẳng)).
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng song song với đường thẳng nào sau đây?
A. AC
B. BD
C. AD
D. SC
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt BC tại E. Gọi C’ là một điểm nằm trên cạnh SC.
a) Tìm giao điểm M của CD và mp(C’AE).
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C’AE).
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và M; N lần lượt là trung điểm của AB; CD . Xác định thiết diện của hình chóp cắt bởi (α) đi qua MN và song song với mặt phẳng (SAD).Thiết diện là hình gì?
A. tứ giác
B. hình thang
C. hình thang cân
D. hình bình hành
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thỏa mãn M A → = 3 M B → . Mặt phẳng (P) qua M và song song với hai đường thẳng SC, BD. Mệnh đề nào sau đây đúng?
A. (P) cắt hình chóp theo thiết diện là một tam giác.
B. (P) không cắt hình chóp.
C. (P) cắt hình chóp theo thiết diện là một ngũ giác.
D. (P) cắt hình chóp theo thiết diện là một tứ giác.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với AI = x (0 < 0 < a). Lấy là mặt phẳng đi qua I và song song với mặt phẳng (SBD).
a) Xác định thiết diện của mặt phẳng với hình chóp S.ABCD.
b) Tìm diện tích S của thiết diện ở câu a) theo a, b, x. Tìm x để S lớn nhất.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Đường thẳng qua M song song với AB cắt CI tại N. Chứng minh rằng NG // (SCD).
c) Chứng minh rằng MG // (SCD).
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên cạnh AB sao cho M A A B = x , 0< x < 1. . Biết rằng mặt phẳng α qua M và song song với (SBC) chia khối chóp S. ABCD thành hai phần trong đó phần chứa điểm A thể tích bằng 4 27 V . Tính giá trị của biểu thức 1 - x 1 + x
A. 1 2
B. 1 5
C. 1 3
D. 3 5
Cho hình chóp S ABCD có đáy ABCD là một tứ giác . Gọi O là giao điểm của 2 đường chéo, AC và BD ở mặt đáy, M là điểm nằm trên đường chéo AC hãy vẽ thiết diện của hình chóp cắt bởi mp qua M, song song với BD và song song với SA trong các trường hợp a. M là trung điểm của AO b. M là trung điểm của CO.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua trung điểm F của cạnh AB, song song với BD và SA là hình gì?
A. Lục giác
B. Tam giác
C. Tứ giác
D. Ngũ giác
Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) di động luôn đi qua A và song song với BD cắt SB, SC, SD theo thứ tự E, F, G. Mặt phẳng (Q) qua EC và song song với BD cắt SA tại H. Chứng minh rằng HF luôn song song với 1 đường thẳng cố định khi (P) thay đổi.