Bài 1:cho biểu thức: A=(a-b) - (2c-4a) + 3c
a.Thu gọn biểu thức A
b.Khi a=12;b=60;c=-135
hãy tính giá trị A.
Bài 2:chứng minh đẳng thức:
a.(a-b)+(c-d)-(a+c)=-(b+d)
b. (a-b)-(c-d)+(b+c)=a-d
Thu gọn biểu thức sau
a) 3a + 4b - 5c - 2a - 3b + 5c
b) 7a + 3b - 4c - 3a+ 2b - 2c - 4a + b - 2c
a) 3a + 4b - 5c - 2a - 3b + 5c
= ( 3a - 2a ) + ( 4b - 3b ) - ( 5c - 5c )
= a + b
b) 7a + 3b - 4c - 3a + 2b - 2c - 4a + b - 2c
= ( 7a - 3a - 4a ) + ( 3b + 2b + b ) - ( 4c + 2c + 2c )
= 6b - 8c
a) 3a + 4b - 5c - 2a - 3b + 5c
= (3a - 2a) + (4b - 3b) - (5c - 5c)
= a + b - 0 = a + b
b) 7a + 3b - 4c - 3a + 2b - 2c - 4a + b - 2c
= (7a - 3a - 4a) + (3b + 2b + b) - ( 4c + 2c + 2c)
= 0 + 6b - 8c = 6b - 8c
a)
3a + 4b - 5c - 2a - 3b + 5c
=( 3a - 2a ) + ( 4b - 3b ) + ( -5c + 5c )
= a + b
b)
7a + 3b - 4c - 3a + 2b - 2c - 4a + b - 2c
=( 7a - 3a - 4a ) + ( 3b + 2b + b ) + ( -4c - 2c - 2c )
= 6b + (-8c)
Cho số thực dương a. Rút gọn biểu thức 4 a - 9 a - 1 2 a 1 2 - 3 a - 1 2 + a - 4 + 3 a - 1 a 1 2 - a - 1 2
A. 9 a 1 2
B. 9a
C. 3a
D. 3 a 1 2
4
a
-
9
a
-
1
2
a
1
2
-
3
a
-
1
2
+
a
-
4
+
3
a
-
1
a
1
2
-
a
-
1
2
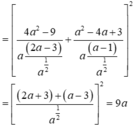
Chọn B
Bài 1: Cho a+b+c=0; rút gọn biểu thức A= a^2/(a^2-b^2-c^2) + b^2/(b^2-c^2-a^2) + c^2/(c^2-b^2-a^2)
Bài 2: Cho abc=2; rút gọn A= a/(ab+a+2) + b/(bc+b+1) + 2c/(ac+2c+2)
Bài 1
Cho biểu thức : A= (2x-1)(4x2+2x+1)-7(x3+1)
a) rút gọn biểu thúc a
B) tính giá trị biểu thức a tại x=-1/2
C) tìm các giá trị nguyên của x để A có giá trị là số nguyên tố
a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=8x^3-1-7x^3-7=x^3-8\)
b: Thay x=-1/2 vào A, ta được:
\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
Bài 1
Cho biểu thức : A= (2x-1)(4x2+2x+1)-7(x3+1)
a) rút gọn biểu thúc a
B) tính giá trị biểu thức a tại x=-1/2
C) tìm các giá trị nguyên của x để A có giá trị là số nguyên tố
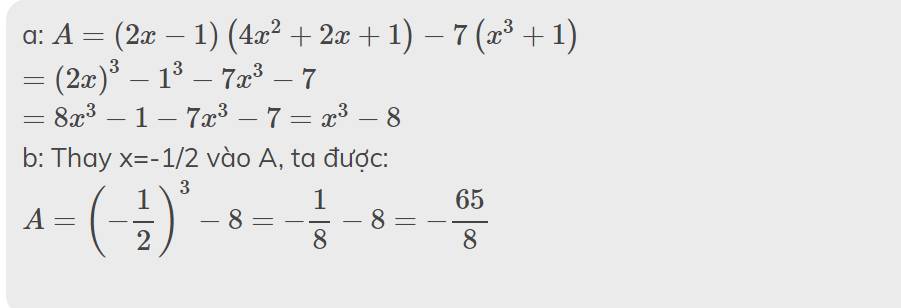
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
Để A là số nguyên tố thì x-2=1
=>x=3
Rút gọn biểu thức P = a - 3 - 4 a - 1 a 1 2 - 4 a - 1 2 - 1 a - 1 2 với a là một số thực dương
A. P = a
B. P = a - 1 2
C. P = a - 1
D. P = a 1 2
Đáp án B
P = a − 3 − 4 a − 1 a 1 2 − 4 a − 1 2 − 1 a − 1 2 = a 1 2 − 3 a − 1 2 − 4 a − 3 2 − a 1 2 + 4 a − 1 2 a − 1 2 ( a 1 2 − 4 a − 1 2 ) = a − 1 2 − 4 a − 3 2 1 − 4 a − 1 = a − 1 2
rút gọn biểu thức:
A=-(-2a+3b-5c)+(-5b+4a-2c)-(3c-4b-7a)
A = 2a-3b+5c-5b+4a-2c-3c+4b+7a = 13a-4b
k mk nha
A=-(-2a+3b-5c)+(-5b+4a-2c)-(3c-4b-7a)
=2a-3b+5c-5b+4a-2c-3c+4b+7a
=13a-4b.
cho abc=2. rút gọn biểu thức:
a/(ab+a+2)+b/(bc+b+1)+2c/(ac+2c+2)
\(\frac{a}{ab+a+2}\)+ \(\frac{b}{bc+b+1}\)+ \(\frac{2c}{ac+2c+2}\)
= \(\frac{a}{ab+a+2}\)+ \(\frac{ab}{a\left(bc+b+1\right)}\)+ \(\frac{2abc}{ab\left(ac+2c+2\right)}\)
= \(\frac{a}{ab+a+2}\)+ \(\frac{ab}{abc+ab+a}\)+ \(\frac{2abc}{a^2bc+2abc+2ab}\)
= \(\frac{a}{ab+a+2}\)+ \(\frac{ab}{ab+a+2}\)+ \(\frac{2}{ab+a+2}\) (vì abc = 2 )
= \(\frac{ab+a+2}{ab+a+2}\)= 1
Cho abc=2. Rút gọn biểu thức: \(M=\dfrac{a}{ab+a+2}+\dfrac{b}{bc+b+1}+\dfrac{2c}{ac+2c+2}\)
M\(=\dfrac{a}{ab+a+2}+\dfrac{b}{bc+b+1}+\dfrac{2c}{ac+2c+2}\)
\(M=\dfrac{a}{ab+a+abc}+\dfrac{b}{bc+b+1}+\dfrac{2bc}{b\left(ac+2c+2\right)}\)
M = \(\dfrac{a}{a\left(b+1+bc\right)}+\dfrac{b}{b+1+bc}+\dfrac{2bc}{abc+2bc+2b}\)
M=\(\dfrac{1}{b+1+bc}+\dfrac{b}{b+1+bc}+\dfrac{2bc}{2+2bc+2b}\)
M = \(\dfrac{1+b}{b+1+bc}+\dfrac{2bc}{2\left(1+bc+b\right)}\)
M = \(\dfrac{1+b}{b+1+bc}+\dfrac{bc}{b+1+bc}=\dfrac{1+b+bc}{b+1+bc}=1\)