Cho tam giác ABS có a =100 ; b=20
a) so sánh các cạnh của tam giác ABC
b) kẻ AH vuông góc vs BC tại H. so sánh HB và HC
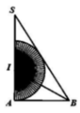
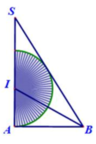
Cho tam giác SAB vuông tại A, ∠ A B S = 60 ° . Phân giác của góc ∠ A B S cắt SA tại I. Vẽ nửa đường tròn tâm I, bán kính IA (như hình vẽ). Cho miền tam giác SAB và nửa hình tròn quay xung quanh trục SA tạo nên các khối tròn xoay có thể tích tương ứng là V1, V2. Khẳng định nào sau đây là đúng?
A. V 1 = 4 9 V 2
B. V 1 = 3 2 V 2
C. V 1 = 3 V 2
D. V 1 = 9 4 V 2
Quay miền tam giác SAB quanh cạnh SA ta được khối nón có chiều cao h = SA , bán kính đáy R = A B .
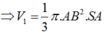
Quay nửa hình tròn quanh cạnh SA ta được khối cầu có bán kính IA.
Áp dụng tính chất đường phân giác ta có:
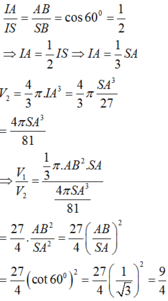
Chọn D.
Cho tam giác SAB vuông tại A, ABS = 60 ° đường phân giác trong của ABS cắt SA tại điểm I. Vẽ nửa đường tròn tâm I bán kính IA (như hình vẽ). Cho ∆ S A B và nửa đường tròn trên quay quanh cạnh SA tạo nên các khối tròn xoay tương ứng có thể tích V 1 , V 2 . Khẳng định nào dưới đây đúng?
A. 4 V 1 = 9 V 2
B. 9 V 1 = 4 V 2
C. V 1 = 3 V 2
D. 2 V 1 = 3 V 2
Đáp án A.
Đặt SA = h tam giác SAB vuông tại A ⇒ A B = S A tan 60 ° = h 3 .
Tam giác IAB vuông tại A ⇒ tan I B A ^ = I A A B ⇒ I A = h 3 .
Khi quay tam giác SAB quay trục SA, ta được khối nón có chiều cao h, bán kính r = h 3 ,
Và quay nửa đường tròn quanh trục SA, ta được khối cầu có bán kính R = h 3 .
Vậy V 1 = 1 3 πr 2 h = 1 3 π . h 3 2 h = πh 3 9 V 2 = 4 3 πR 2 = 4 3 π h 3 3 = 4 πh 3 81 ⇒ V 1 V 2 = 1 9 : 4 81 = 9 4 ⇒ 4 V 1 = 9 V 2 .
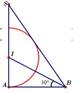
Cho tam giác SAB vuông tại A, ABS= 60 o đường phân giác trong của ABS cắt SA tại điểm I. Vẽ nửa đường tròn tâm I bán kính IA (như hình vẽ). Cho △ S A B và nửa đường tròn trên quay quanh cạnh SA tạo nên các khối tròn xoay tương ứng có thể tích V 1 , V 2 Khẳng định nào dưới đây đúng?

![]()
![]()
![]()
![]()
Cho tam giác SAB vuông tại A, A B S ^ = 60 ° . Phân giác của góc A B S ^ cắt SA tại I. Vẽ nửa đường tròn tâm I, bán kính IA (như hình vẽ). Cho miền tam giác SAB và nửa hình tròn quay xung quanh trục SA tạo nên các khối tròn xoay thể tích tương ứng là V 1 , V 2 . Khẳng định nào sau đây đúng?
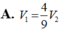
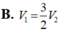
![]()
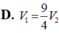
tính diện tích của tam giác abs có góc a = 90 độ , ab = 4cm ac= 5cm,
Diện tích tam giác abc là \(S_{abc}=\frac{ab.ac}{2}=\frac{4.5}{2}=10cm^2\)
Cho tam giác ABS vuông tại A. Trên cạnh AC lấy điểm E sao cho góc EBA=1/3B, trên tia đối tia EB lấy điểm D sao cho ED=BC. Chứng minh: tam giác CED là tam giác cân
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại A, độ dài \(AB=AC=a\).
Biết rằng \(\Delta SAB\) có góc \(\widehat{ABS}=60^0\) và nằm trong mặt phẳng vuông góc với mặt đáy.
Tính khoảng cách từ điểm A đến mp(SBC) theo \(a\) .
P/s: em nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em với ạ, em cám ơn nhiều ạ!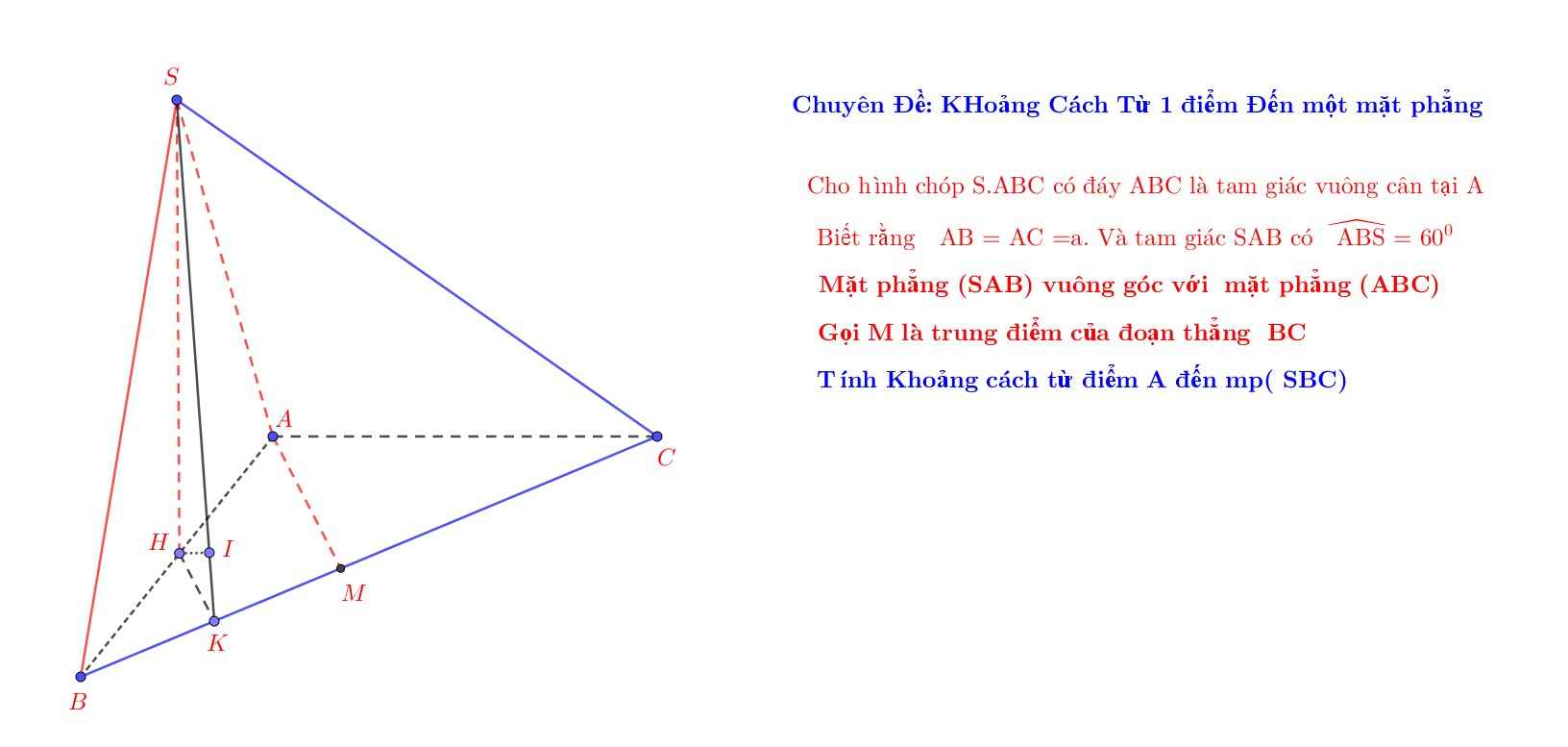
Hình bạn tự vẽ nha mình biếng á chứ khog có j đou=)
Ta có : \(\left\{{}\begin{matrix}CA\perp AB\\\left(ABC\right)\perp\left(SAB\right)\\\left(ABC\right)\cap\left(SAB\right)=AB\end{matrix}\right.\) \(\Rightarrow CA\perp\left(SAB\right)\)
Kẻ \(AK\perp SB\) và \(AH\perp CK\) tại H.
Ta có : \(\left\{{}\begin{matrix}SB\perp AK\\SB\perp CA\end{matrix}\right.\) \(\Rightarrow SB\perp\left(ACK\right)\Rightarrow SB\perp AH\)
Do : \(\left\{{}\begin{matrix}AH\perp CK\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=AH\)
Xét t/g ABK , ta có : AK = AB
=> \(sin\widehat{ABK}=\alpha sin60^o=\dfrac{a\sqrt{3}}{2}\)
Xét t/g ACK , ta có : \(\dfrac{1}{AH^2}=\dfrac{1}{AK^2}+\dfrac{1}{AC^2}=\dfrac{7}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{21}}{7}\)
cho tam giác abs cân tại A . Đường phân giác BE,kẻ EH vuông góc với BC (h thuộc bc) gọi k là giao điểm của ab và HE
a, chứng minh BE là Đường trung trực của đoạn AH
b,cm Ek=EC
c, so sánh AE và EC
cho a,b,c la cac so thuc bat ki .CMR 1, Abs(b+c-a)+Abs(c+a-b)+Abs(a+b-c)>=2*(Abs(a)+Abs(b)+Abs+(c))
2, Abs(a)+Abs(b)+Abs(c)+Abs(a+b+c)>= Abs(a+b)+Abs(b+c)+Abs(c+a)