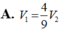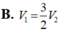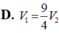Các câu hỏi tương tự
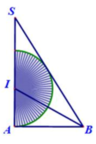
Tam giác vuông cân ABC ngoại tiếp đường tròn tâm I (như hình vẽ). Cho nửa đường tròn (phần gạch sọc) và tam giác AHC quay quanh AH tạo thành các khối tròn xoay quanh có thể tích là
V
1
,
V
2
. Tính
k
V
1
V
2
.
Đọc tiếp
Tam giác vuông cân ABC ngoại tiếp đường tròn tâm I (như hình vẽ). Cho nửa đường tròn (phần gạch sọc) và tam giác AHC quay quanh AH tạo thành các khối tròn xoay quanh có thể tích là V 1 , V 2 . Tính k = V 1 V 2 .

![]()
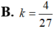
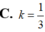
![]()
Cho đường tròn (C) có tâm I, bán kính
R
a
. Gọi M là điểm nằm ngoài (C) và
I
M
a
3
; A là điểm thuộc (C) và MA tiếp xúc với (C); H là hình chiếu của A trên đường thẳng IM. Tính theo a thể tích V của khối tròn xoay tạo bởi hình tam giác MAH quay xung quanh trục IM
Đọc tiếp
Cho đường tròn (C) có tâm I, bán kính R = a . Gọi M là điểm nằm ngoài (C) và I M = a 3 ; A là điểm thuộc (C) và MA tiếp xúc với (C); H là hình chiếu của A trên đường thẳng IM. Tính theo a thể tích V của khối tròn xoay tạo bởi hình tam giác MAH quay xung quanh trục IM
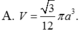
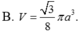
![]()
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R 3cm, góc ở đỉnh hình nón là
φ
120
°
. Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng: A. 3
3
c
m
2
B. 6
3
c
m
2
C. 6
c...
Đọc tiếp
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R = 3cm, góc ở đỉnh hình nón là φ = 120 ° . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng:
A. 3 3 c m 2
B. 6 3 c m 2
C. 6 c m 2
D. 3 c m 2
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y
x
,
y
0
và
x
4
quanh trục Ox. Đường thẳng x a (0 a 4 cắt đồ thị hàm số
y
x
tại M (hình vẽ). Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V2V1. Khi đó A. . B. . C. . D. .
Đọc tiếp
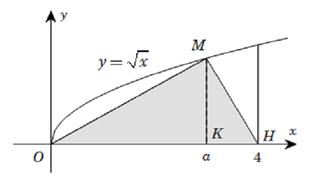
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = x , y = 0 và x = 4 quanh trục Ox. Đường thẳng x = a (0< a< 4 cắt đồ thị hàm số y = x tại M (hình vẽ). Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V=2V1. Khi đó
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R3cm, góc ở đỉnh của hình nón là
φ
120
0
. Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
Đọc tiếp
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh của hình nón là φ = 120 0 . Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
![]()
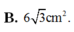
![]()
![]()
Cho tam giác đều ABC có đỉnh A(5;5) nội tiếp đường tròn tâm I đường kính AA, M là trung điểm BC. Khi quay tam giác ABM cùng với nửa hình tròn đường kính AA xung quanh đường thẳng AM (như hình vẽ minh họa), ta được khối nón và khối cầu có thể tích lần lượt là
V
1
v
à
V
2
. Tỷ số ...
Đọc tiếp
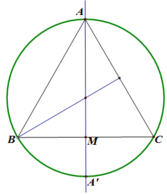
Cho tam giác đều ABC có đỉnh A(5;5) nội tiếp đường tròn tâm I đường kính AA', M là trung điểm BC. Khi quay tam giác ABM cùng với nửa hình tròn đường kính AA' xung quanh đường thẳng AM (như hình vẽ minh họa), ta được khối nón và khối cầu có thể tích lần lượt là V 1 v à V 2 . Tỷ số V 1 V 2 bằng
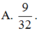
![]()
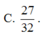
![]()
Cho hình nón đỉnh S có đáy là đường tròn tâm O và bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng
R
2
2
, thể tích khối nón đã cho bằng
Đọc tiếp
Cho hình nón đỉnh S có đáy là đường tròn tâm O và bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng R 2 2 , thể tích khối nón đã cho bằng
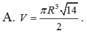
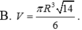
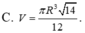
![]()
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng
R
2
2
, thể tích khối nón đã cho bằng
Đọc tiếp
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy 2 điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng R 2 2 , thể tích khối nón đã cho bằng
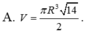
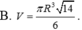
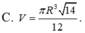
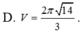
cho hình nón đỉnh s có đáy là hình tròn tâm o. dựng hai đường sinh SA và SB,biết tam giác SAB vuông và có diên tích 4a^2. góc tạo bởi trục SO và mặt phẳng SAB bằng 30 độ.thể tích hình nón bằng