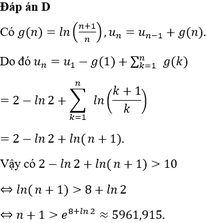1. Tìm 2 số tự nhiên nhỏ nhất a và b thoả mãn ƯCLN ( a ; b) = 12 và a - b = 84

Những câu hỏi liên quan
tìm phân số a/b sao cho a là số tự nhiên nhỏ nhất thoả mãn 4/15 < a/b < 1/3
tìm các số tự nhiên nhỏ nhất lớn hơn 1 thoả mãn : a^2017=b^2018
mk nghĩ là 3^2017=2^2018
đây là ý kiến riêng của mk
k cho mk nha!!!
Đúng 0
Bình luận (0)
1. Tìm số tự nhiên nhỏ nhất, biết số đó chia cho 3,4,5,6 đều dư 2, còn chia cho 7 thì dư 3.
2. Tìm 2 số tự nhiên biết tổng ƯCLN và BCNN của chúng bằng 23.
3. Tìm các số tự nhiên a,b thỏa mãn:\(\frac{5a+7b}{6a+5b}=\frac{29}{28}\)và (a,b)=1
a)Tìm hai số tự nhiên a,b biết BCNN(a,b)=300;ƯCLN(a,b)=15
b)tìm cái số nguyên x,y thoả mãn: (x+1)(2y-5) =8
Bài 2. Tìm các số tự nhiên x biết:
a) x:15, x:35, x:42 và 250 < x < 850 .
b) x là số nhỏ nhất khác 0 thoả mãn x:15 và x:115;
c) (x−1)52,(x−1) 35 và 1000 < x < 2000
a) \(x⋮15;x⋮35;x⋮42\&250< x< 850\) (sửa dấu chia thành chia hết)
\(BCNN\left(15;35;42\right)=210\)
\(\Rightarrow x\in BC\left(15;35;42\right)=\left\{0;210;420;630;840;...\right\}\)
mà \(250< x< 850\)
\(\Rightarrow x\in\left\{420;630;840\right\}\)
b) x nhỏ nhất khác 0 thỏa mãn \(x⋮15;x⋮115\)
\(BCNN\left(15;115\right)=345\)
Vậy \(x\in\left\{345\right\}\) thỏa mãn đề bài
Đúng 1
Bình luận (0)
phần c lỗi nha ạ, mình sửa lại
c) (x−1) chia hết 52,(x−1) chia hết 35 và 1000 < x < 2000
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1: số trong lớp không lớn hơn 30 hỏi có thể là bao nhiêu biết rằng khi xếp hàng 3 thì dư 2 bàn khi xếp hàng 5 thì dư 1 bànBài 2:Tìm số tự nhiên a nhỏ nhất biết rằng số đó chia cho 3,4,5 dư 1 và chia hết cho 11Bài 3: Tìm số tự nhiên a và b ab biết rằng BCNN(a,b)+ƯCLN(a,b)19 BCNN(a,b)-ƯCLN(a,b)3Bài 4: Tìm số tự nhiên a,b,c biết 16a25b30c. a,b,c là các số tự nhiên nhỏ nhất khác 0
Đọc tiếp
Bài 1: số trong lớp không lớn hơn 30 hỏi có thể là bao nhiêu biết rằng khi xếp hàng 3 thì dư 2 bàn khi xếp hàng 5 thì dư 1 bàn
Bài 2:Tìm số tự nhiên a nhỏ nhất biết rằng số đó chia cho 3,4,5 dư 1 và chia hết cho 11
Bài 3: Tìm số tự nhiên a và b a<b biết rằng BCNN(a,b)+ƯCLN(a,b)=19 BCNN(a,b)-ƯCLN(a,b)=3
Bài 4: Tìm số tự nhiên a,b,c biết 16a=25b=30c. a,b,c là các số tự nhiên nhỏ nhất khác 0
tìm stn n nhỏ nhất thoả mãn n=3a^3=4b^4 với a,b thuộc các số tự nhiên khác 0
a) Chứng tỏ rằng: 102120 +2120 chia hết cho 30
b) Cho a vá b là hai số tự nhiên không nguyên tố cùng nhau và thoả mãn :
a=2n+3 , b=5n+2 (n ϵ N) . Tìm ƯCLN(a,b)
giúp em với ạ
a) Dễ thấy P = 102120 + 2120
= 102120 + 212.10
= 10(102119 + 212)
=> P \(⋮10\)
Lại có P = 102120 + 2120
= 10(102119 + 212)
= 10.(1000...00 + 212)
2119 số 0
= 10.1000...0212
2116 số 0
Tổng các chữ số của số S = 1000...0212 (2116 chữ số 0)
là 1 + 0 + 0 + 0 +.... + 0 + 2 + 1 + 2 (2116 hạng tử 0)
= 1 + 2 + 1 + 2 = 6 \(⋮3\)
=> S \(⋮3\Rightarrow P=10S⋮3\)
mà \(\left\{{}\begin{matrix}P⋮10\\P⋮3\\\left(10,3\right)=1\end{matrix}\right.\Rightarrow P⋮10.3\Rightarrow P⋮30\)
Đúng 1
Bình luận (0)
Gọi (a,b) = d \(\left(d\inℕ^∗;d\ne1\right)\)
=> \(\left\{{}\begin{matrix}a⋮d\\b⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\5n+2⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}5.(2n+3)⋮d\\2.(5n+2)⋮d\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}10n+15⋮d\left(1\right)\\10n+4⋮d\left(2\right)\end{matrix}\right.\)
Lấy (1) trừ (2) ta được
(10n + 15) - (10n + 4) \(⋮d\)
<=> 11 \(⋮d\)
\(\Leftrightarrow d\in\left\{1;11\right\}\) mà d \(\ne1\)
<=> d = 11
Vậy (a;b) = 11
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
thoả mãn
u
n
u
n
-
1
+
l
n
(
n
+
1
n
)
,
∀
n
≥
2
và
u
1
2...
Đọc tiếp
Cho dãy số ( u n ) thoả mãn u n = u n - 1 + l n ( n + 1 n ) , ∀ n ≥ 2 và u 1 = 2 . Tìm số tự nhiên n nhỏ nhất để u n > 10 .
A. 5962.
B. 5960.
C. 5963.
D. 5961.