1/.Tìm n thuộc N để A chia hết B:
A= (7xn-1y5-5x3y4)
B= 5x2yn
2/. Cho biết a+b+c=1; a3+b3+c3 =1
Chứng minh a2005+b2005+c2005 =1
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7 x n - 1 y 5 - 5 x 3 y 4 ; B = 5 x 2 y n
Ta có
A : B = ( 7 x n - 1 y 5 - 5 x 3 y 4 ) : ( 5 x 2 y n ) = 7 / 5 x n - 3 y 5 - 5 - x y 4 - n
Theo đề bài đa thức A chia hết cho đơn thức B
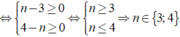
Vậy giá trị n cần tìm là n∈{3; 4}
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7 x n - 1 y 5 - 5 x 3 y 4 ;
B = 5 x 2 y n
1. Tìm x, y để:
f)x-y=6 và 4x7+1y5 chia hết cho 9
g)2xây chia hết cho 4 và 11
2. Cho n thuộc về số tự nhiên, chứng minh rằng:
c)n*(n+1)*(2n+1) chia hết cho 3
4. Tìm số tự nhiên lớn nhất có 3 chữ số chia 4 và chia 25 dư 8
5. Tìm a biết:
a)32a1 chia hết cho 7
b)1a25 chia hết cho 13
c)a38 chia hết cho 6
1.
g/ 2xy chia hết cho 4 và 11.
Để 2xy chia hết cho 4 thì xy chia hết cho 4.
xy c {12 ; 16 ; 20 ; ... ; 96}
- 2xy = 212 không chia hết cho 11.
- 2xy = 216 không chia hết cho 11.
- 2xy = 220 chia hết cho 11.
Vậy, 2xy = 220.
5/
c) a38 chia hết cho 6
6 = 2 . 3
Để a38 chia hết cho 6 thì a38 chia hết cho 2 và 3.
a38 đã thoả mãn điều kiện chia hết cho 2 vì tận cùng của số đó là số 8.
Ta có: a38 = a + 3 + 8 = a + 11 => a c {1 ; 4 ; 7}
Vậy, a38 c {138 ; 438 ; 738}
Tìm a để A chia hết cho B:A=49x^2+a×x+b ;B=7x-1
A chia hết cho B
=>\(49x^2+ax+b⋮7x-1\)
=>\(49x^2-7x+\left(a+7\right)x-\dfrac{1}{7}\left(a+7\right)+b+\dfrac{1}{7}\left(a+7\right)⋮7x-1\)
=>\(7x\left(7x-1\right)+\dfrac{1}{7}\left(a+7\right)\left(7x-1\right)+b+\dfrac{1}{7}\left(a+7\right)=0\)
b+1/7(a+7)=0
=>(a+7)+7b=0
=>a=-7b-7
Vậy: Với a,b là các số nguyên sao cho a=-7b-7 thì A chia hết cho B
1. Cho A =abcc ; tìm A biết: A: 5 và a;b;c thuộc { 1;5;9}
2. cho A= n2 + 1 ( n thuộc N)
a/ tìm 5 giá trị của n để A chia hết cho 5
b/ tìm n để A chia hết cho 2
3. tìm số tự nhiên có 3 chữ số giống nhau biết số đó chia 5 dư 2 và chia 2 dư 1
1, Để A chia hết cho 5 thì chữ số tận cùng của A là 0 và 5
\(\Rightarrow\)c phải là 5
Chữ số tận cùng là 5 chia hết cho 5 rồi thì còn lại 2 số đầu có thể xếp lên a hoặc là b
\(\Rightarrow\)A có thể là 1955 hoặc là 9155
Tìm n thuộc N biết
(n^2+7xn+11) chia hết cho ( n+1)
n(n + 1) chia hết cho n + 1
n2 + n chia hết cho n + 1
=> n2 +7n + 11 - n2 + n chia hết cho n + 1
8n + 11 chia hết cho n + 1
8n + 8 + 3 chia hết cho n + 1
3 chia hết cho n + 1
n + 1 thuộc Ư(3) = {-3 ; -1 ; 1 ; 3}
n + 1 =-3 => n =-4
n + 1 = -1 => n = -2
n + 1 = 1 => n = 0
n +1= 3 => n = 2
Vậy n = 0;2
1 tìm n thuộc z biết
a, 7 chia hết n-2
2 tìm n thuộc z biết
a, 2n+5 chia hết cho n-1
b, n+3 chia hết cho 2n -1
3 tìm n thuộc z biết
a, 2n-5 chia hết cho n+1 và n+1 chia hết cho 2n+5
b, 3n+2 chia hết cho n-2 và n-2 chia hết cho 3n+2
1. Tìm n thuộc Z để giá trị của biểu thức A= n^3 + 2n^2 - 3n + 2 chia hết cho giá trị của biểu thức B= n^2 - n
2.a. Tìm n thuộc N để n^5 + 1 chia hết cho n^3 + 1
b. Giải bài toán trên nếu n thuộc Z
3. Tìm số nguyên n sao cho:
a. n^2 + 2n - 4 chia hết cho 11
b. 2n^3 + n^2 + 7n + 1 chia hết cho 2n - 1
c.n^4 - 2n^3 + 2n^2 - 2n + 1 chia hết cho n^4 - 1
d. n^3 - n^2 + 2n + 7 chia hết cho n^2 + 1
4. Tìm số nguyên n để:
a. n^3 - 2 chia hết cho n - 2
b. n^3 - 3n^2 - 3n - 1 chia hết cho n^2 + n + 1
c. 5^n - 2^n chia hết cho 63
1) Cho A= (3n - 13)/(n - 1) (n thuộc Z )
a) Tìm n nguyên để A nguyên.
b) Tìm n nguyên để A là phân số tối giản.
2. Cho a,b thuộc N. Chứng minh rằng: 4a + b chia hết cho 5 và a + 4b chia hết cho 5
a, Tìm chữ số tận cùng của số tự nhiên a để có ( a mũ 2 + 1 ) chia hết cho 2.
b, Cho n là số tự nhiên lẻ, tìm số dư khi chia n mũ 2 cho 8
c, Cho a,b thuộc N, chứng tỏ rằng ab . ( a+b) chia hết cho 2
d, Tìm x,y thuộc N biết xy. (x+y) = 570319