Cho hình thang ABCD(AB//CD) có hai đường chéo AC và BD cắt nhau tại O . Cho biết SAOB =a2 ;SCOD = b2 . Tính diện tích hình thang ABCD theo a,b

Những câu hỏi liên quan
cho hình thang ABCD có đáy nhỏ AB=1/3CD .Hai đường chéo AC và BD cắt nhau ở O biết SAOB=4CM vuông.tính SABCD
Cho hình thang ABCD có AB//CD và 2 đường chéo AC, BD cắt nhau tại O chứng minh
a, SAOB + SCOD >=1/2SABCD
b, Điều kiện nào của hình thang ABCD thì SAOB +SCOD đạt GTNN
cho hình thang ABCD .đáy AB=2/3CD. hai đường chéo AC và BD cắt nhau tại O. sAOB kém sCOD là 3,5 cm2. tính sABCD
1.Cho hình thang ABCD có hai đáy AB và CD, hai đường chéo cách nhau tại O, biết diện tích tam giác AOB bằng 4 cm2 , diện tích tam giác BOC bằng 9cm2. Tính diện tích hình thang ABCD.2.Cho hình thang ABCD có hai đường chéo AC và BD cắt nhau tại O và AO bằng 1/2 OC. Diện tích hình tam giác BOC là 12 cm2. Tính diện tích hình thang ABCD?3.Cho hình thang ABCD. Đáy lớn CD gấp đôi đáy bé AB. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác BOC là 34,5 cm2. Tính diện tích hình thang ABCD.4...
Đọc tiếp
1.Cho hình thang ABCD có hai đáy AB và CD, hai đường chéo cách nhau tại O, biết diện tích tam giác AOB bằng 4 cm2 , diện tích tam giác BOC bằng 9cm2. Tính diện tích hình thang ABCD.
2.Cho hình thang ABCD có hai đường chéo AC và BD cắt nhau tại O và AO bằng 1/2 OC. Diện tích hình tam giác BOC là 12 cm2. Tính diện tích hình thang ABCD?
3.Cho hình thang ABCD. Đáy lớn CD gấp đôi đáy bé AB. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác BOC là 34,5 cm2. Tính diện tích hình thang ABCD.
4.Cho hình thang ABCD. Đáy lớn CD, đáy bé AB. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác ABG là 34,5 cm2 và diện tích tam giác DGC là 138 cm2. Tính diện tích hình thang ABCD.
[ Làm chi tiết giúp mình nhé!]
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)
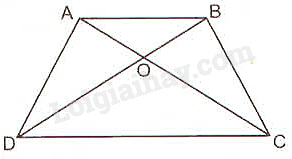
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
Đúng 0
Bình luận (0)
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)

Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
Đúng 0
Bình luận (0)
Cho hình thang ABCD có đáy AB = CD. Đường chéo AC và BD cắt nhau tại O. Tính biết diện tích hình tam giác AOD. Biết diện tích hình thang ABCD bằng 100cm2
Cho hình thang ABCD có đáy AB = CD. Đường chéo AC và BD cắt nhau tại O. Tính biết diện tích hình tam giác AOD. Biết diện tích hình thang ABCD bằng 100cm2
AB=CD AB//CD
=>ABCD là hbh
=>S AOD=1/2*S ADC=1/4*S ABCD=25cm2
Đúng 0
Bình luận (0)
1. Cho hình thang ABCD với hai đáy AB, CD. Hai đường chéo AC, BD
cắt nhau tại E. Chứng minh rằng diện tích AED = diện tích BEC.
2.Cho hình thang ABCD với hai đáy AB, DC và biết DC = 3AB. Hai
đường chéo AC cắt BD tại E. Chứng minh rằng diện tích ADE = diện tích BCE
và tính tỷ số \(\dfrac{EA}{EC}\)
1. Cho hình thang ABCD với hai đáy AB, CD. Hai đường chéo AC, BD
cắt nhau tại E. Chứng minh rằng diện tích AED = diện tích BEC.
2.Cho hình thang ABCD với hai đáy AB, DC và biết DC = 3AB. Hai
đường chéo AC cắt BD tại E. Chứng minh rằng diện tích ADE = diện tích BCE
và tính tỷ số \(\dfrac{EA}{EC}\)



















