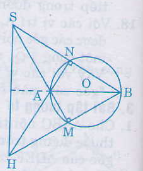
BM ⊥ SA ( = vì là góc nội tiếp chắn nửa đường tròn).

Tương tự, có: AN ⊥ SB

Như vậy BM và AN là hai đường cao của tam giác SAB và H là trực tâm.

Suy ra SH ⊥ AB.

(Trong một tam giác ba đường cao đồng quy)

a) Xét (O) có 

\(\widehat{AED}\) là góc nội tiếp chắn \(\stackrel\frown{AD}\)

\(\widehat{DAM}\) là góc tạo bởi tia tiếp tuyến AM và dây cung AD

Do đó: \(\widehat{AED}=\widehat{DAM}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)

\(\Leftrightarrow\widehat{AEM}=\widehat{DAM}\)

Xét ΔAEM và ΔDAM có 

\(\widehat{AEM}=\widehat{DAM}\)(cmt)

\(\widehat{AMD}\) chung

Do đó: ΔAEM∼ΔDAM(g-g)

⇒\(\dfrac{ME}{MA}=\dfrac{MA}{MD}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(ME\cdot MD=MA^2\)(đpcm)

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAOM vuông tại A có AH là đường cao ứng với cạnh huyền AO, ta được:

\(MH\cdot MO=AM^2\)

mà \(ME\cdot MD=AM^2\)(cmt)

nên \(MD\cdot ME=MH\cdot MO\)(đpcm)

Nènnfkgngngnldkduejebdnxncbxbdbjdkeo

a:

Xét (O) có

AB,AC là các tiếp tuyến

Do đó: BA=AC

Xét (O) có

\(\widehat{ABD}\) là góc tạo bởi tiếp tuyến BA và dây cung BD

\(\widehat{BED}\) là góc nội tiếp chắn cung BD

Do đó: \(\widehat{ABD}=\widehat{BED}\)

=>\(\widehat{ABD}=\widehat{AEB}\)

Xét (O) có

\(\widehat{ACD}\) là góc tạo bởi tiếp tuyến CA và dây cung CD

\(\widehat{DEC}\) là góc nội tiếp chắn cung DC

Do đó: \(\widehat{ACD}=\widehat{DEC}\)

=>\(\widehat{ACD}=\widehat{AEC}\)

Xét ΔABD và ΔAEB có

\(\widehat{ABD}=\widehat{AEB}\)

\(\widehat{BAD}\) chung

Do đó: ΔABD đồng dạng với ΔAEB

=>\(\dfrac{BD}{EB}=\dfrac{AB}{AE}=\dfrac{AC}{AE}\left(1\right)\)

Xét ΔACD và ΔAEC có

\(\widehat{ACD}=\widehat{AEC}\)

\(\widehat{CAD}\) chung

Do đó: ΔACD đồng dạng với ΔAEC

=>\(\dfrac{CD}{EC}=\dfrac{AC}{AE}\left(2\right)\)

Từ (1) và (2) suy ra \(\dfrac{BD}{EB}=\dfrac{CD}{EC}\)

=>\(BD\cdot EC=CD\cdot EB\)

b: Gọi giao điểm thứ hai của BI với (O) là F

Xét (O) có

\(\widehat{EBF}\) là góc nội tiếp chắn cung EF

\(\widehat{DBF}\) là góc nội tiếp chắn cung DF

\(\widehat{EBF}=\widehat{DBF}\)

Do đó: \(sđ\stackrel\frown{EF}=sđ\stackrel\frown{DF}\)

Xét (O) có \(\widehat{BID}\) là góc ở trong đường tròn và chắn hai cung BD và FE

nên \(\widehat{BID}=\dfrac{1}{2}\left(sđ\stackrel\frown{BD}+sđ\stackrel\frown{FE}\right)\)

=>\(\widehat{BID}=\dfrac{1}{2}\left(sđ\stackrel\frown{BD}+sđ\stackrel\frown{FD}\right)=\dfrac{1}{2}\cdot sđ\stackrel\frown{BF}\left(3\right)\)

Xét (O) có

\(\widehat{ABF}\) là góc tạo bởi tiếp tuyến BA và dây cung BF

nên \(\widehat{ABF}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BF}\left(4\right)\)

Từ (3) và (4) suy ra \(\widehat{BID}=\widehat{ABF}\)

=>\(\widehat{ABI}=\widehat{AIB}\)

=>AB=AI

mà AB=AC

nên AB=AI=AC

c) OM cắt CD tại F

Ta có OK.OM=OC2=R2OK.OM=OC2=R2

ΔOHM∼ΔOKF⇒OHOK=OMOFΔOHM∼ΔOKF⇒OHOK=OMOF

⇒OF=OK.OMOH=R2OH⇒OF=OK.OMOH=R2OH (không đổi)

mà OF nằm trên đường cố định nên F là điểm cố định khi M thay đổ

c)OM cắt CD tại F

Ta có \(OK.OM=OC^2=R^2\)

\(\Delta OHM~\Delta OKF\Rightarrow\frac{OH}{OK}=\frac{OM}{OF}\)

\(OF=\frac{OK.OM}{OH}=\frac{R^2}{OH}\)( không đổi)

mà OF nằm trên đường cố định nên F là điểm cố định khi M thay đổi

Sao tự hỏi tự trả lời z bạn

hoidap247

Chọn B

b

Co nha ban