Cho hình lăng trụ ABC.A'B'C'. Gọi M là trung điểm của BC; N là điểm trên cạnh CC' sao cho CN = 2 NC'
1) Tìm giao điểm I của AB với (A'MN). Tính IA/IB
2) tìm giao tuyến của (AMC') và (A'NB)
3) Tìm giao tuyến của (ANB) và (MA'C')
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AA' = a 3 , AB = a. Gọi M là trung điểm BC. Tính thể tích V của hình chóp AMB’C’.
A. V = a 3 3 4
B. V = a 3 3
C. V = a 3 4
D. V = a 3 3 2
Cho hình lăng trụ đứng ABC.A'B'C'. Gọi M là trung điểm A'C', I là giao điểm của AM và A'C. Khi đó tỉ số thể tích của khối tứ diện IABC với khối lăng trụ đã cho bằng:
A . 2 3
B . 2 9
C . 4 9
D . 1 2
Đáp án B.
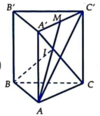
Xét
∆
AA'C có I là trọng tâm, ![]()
Ta có: ![]()
![]()

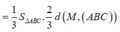
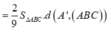
Cho hình lăng trụ đứng ABC.A'B'C'. Gọi M là trung điểm A'C', I là giao điểm của AM và A'C. Khi đó tỉ số thể tích của khối tứ diện IABC với khối lăng trụ đã cho bằng:
A. 2 3
B. 2 9
C. 4 9
D. 1 2
Đáp án B
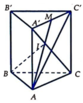
Xét ∆ A A ' C có I là trọng tâm, d ( I , ( A B C ) ) = 2 3 d ( M , ( A B C ) )
Ta có: V A B C . A ' B ' C ' = S A B C . A A ' = S A B C . d A ' ; A B C
V I A B C = 1 3 S ∆ A B C . d I , ( A B C ) = 1 3 S ∆ A B C . 2 3 d ( M , ( A B C ) ) = 2 9 S ∆ A B C . d ( A ' , ( A B C ) )
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy là A B C là tam giác vuông B A = B C = a , cạnh bên AA ' = a 2 .Gọi M là trung điểm của B C . Tính khoảng cách giữa hai đường thẳng A M , B ' C ' .
A. d A M , B ' C = a 7 7
B. d A M , B ' C = a 2 2
C. d A M , B ' C = a 3 3
D. d A M , B ' C = a 5 5
Đáp án là A
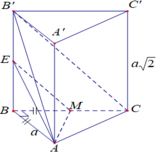
Gọi E là trung điểm của B B ' . Khi đó B ' C / / A M E ⇒ d A M ; B ' C = d B ' C ; A M E .
Mặt khác d B ; A M E = d C ; A M E . Gọi h = d B ; A M E
Vì tứ diện B A M E có B A ; B M ; B E đôi một vuông góc với nhau.
⇒ 1 h 2 = 1 B A 2 + 1 B M 2 + 1 B E 2 ⇒ 1 h 2 = 1 a 2 + 4 a 2 + 2 a 2 = 7 a 2 ⇒ h = a 7 7 ⇒ d B ' C ; A M = a 7 7 .
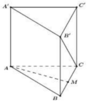
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là:
![]()
![]()
Cho hình lăng trụ ABC.A'B'C' Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số V M N C ' A B C V M N A ' B ' C '
A. 2
B. 1,5
C. 2,5
D. 3
Đáp án A
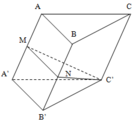
V A A ' B ' C ' = V C ' A B C = V A B B ' C ' = 1 3 V A B C A ' B ' C ' V M N A ' B ' C ' = 1 2 V C ' A B B ' A ' = 1 2 . ( V A A ' B ' C ' + V A B B ' C ' ) = 1 2 . 2 3 V A B C A ' B ' C ' = 1 3 V A B C A ' B ' C ' ⇒ V M N C ' A B C V M N A ' B ' C ' = 2
Cho hình lăng trụ ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số V M N C ' A B C V M N A ' B ' C '
A. 2
B. 1,5
C. 2,5
D. 3
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A , A B C ^ = 30 ° . Gọi M là trung điểm của AB, tam giác MA'C đều cạnh 2 a 3 và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối lăng trụ là ABC.A'B'C'
A. 24 2 a 3 7
B. 24 3 a 3 7
C. 72 3 a 3 7
D. 72 2 a 3 7
Cho hình lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh 3 . Gọi I là trung điểm của cạnh BC. Biết thể tích lăng trụ là V = 6, khoảng cách từ I đến mặt phẳng (A'B'C') là:
A . 8 3
B . 8 3 3
C . 4 3
D . 4 3 3
Cho hình lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh 3 . Gọi I là trung điểm của cạnh BC. Biết thể tích lăng trụ là V=6 , khoảng cách từ I đến mặt phẳng (A'B'C') là:
A. 8 3
B. 8 3 3
C. 4 3
D. 4 3 3